

Next: 6 Convergence to an
Up: Time-periodic solutions
Previous: 4 Decay estimates
(PDF file: paper9.pdf)
5 Compactness of entropy
In this section, we show the compactness of
in
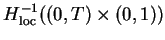 for any smooth entropy pair
for any smooth entropy pair
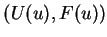 , where
, where 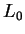 is sufficiently large integer for
(19) and (22).
is sufficiently large integer for
(19) and (22).
For simplify, we set
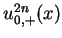 as the function consists
of the step values
as the function consists
of the step values 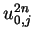
and use notations
and so on.
We consider for a particular entropy pairs
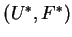 defined by
defined by
Since the approximation
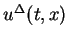 satisfies the equation
(12) almost everywhere,
satisfies the equation
(12) almost everywhere,
where
 is summation for all the shock waves arise in
is summation for all the shock waves arise in
![$[0,T]\times[0,1]$](img183.gif) ,
, ![$[U^\ast]$](img184.gif) and
and ![$[F^\ast]$](img185.gif) is the difference across
the wave, and
is the difference across
the wave, and 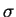 is the speed of it.
Because of
is the speed of it.
Because of
we have
The boundedness of
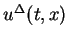
shows that
Hence we obtain the inequality
where 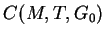 is a constant depends on
is a constant depends on 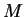 ,
, 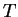 and
and 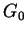 .
.
Let 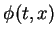 be a function in
be a function in
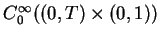 .
The integral
.
The integral
![\begin{displaymath}
\int\hspace{-6pt}\int _{[0,T]\times[0,1]}\{U(u^\Delta )\phi_t+F(u^\Delta )\phi_x\}dtdx\end{displaymath}](img198.gif) |
(28) |
is divided into four parts
where
and
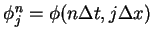 . We estimate
. We estimate 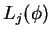
and 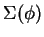
by the similar way in [3] (I).
Hence the integral (28) is the sum of two
linear operators 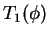 and
and 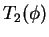 which satisfy
which satisfy
where the constant 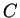 depends on
depends on 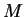 ,
, 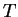 ,
, 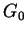 , maximum value of
, maximum value of 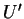 and
and 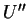 , and
, and 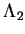 .
This shows the following proposition by the argument in [3]
(I).
.
This shows the following proposition by the argument in [3]
(I).
PROPOSITION 5
For any smooth entropy pair
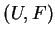
, the set
is relatively compact in
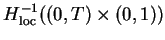
.
Proposition 5 and Tartar's theorem
([15]) yields the existence of subsequence which converges
almost everywhere. It also valid for the initial data
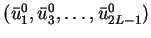 (§4).
(§4).


Next: 6 Convergence to an
Up: Time-periodic solutions
Previous: 4 Decay estimates
Shigeharu TAKENO
15 January 2002
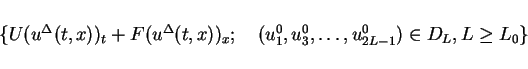
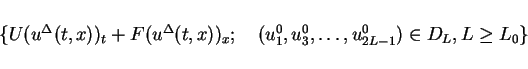
![]() as the function consists
of the step values
as the function consists
of the step values ![]()
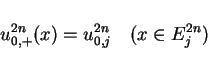
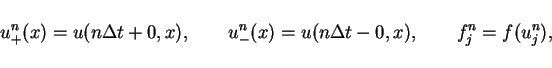
![]() defined by
defined by
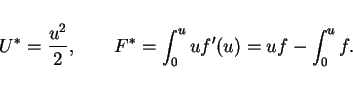
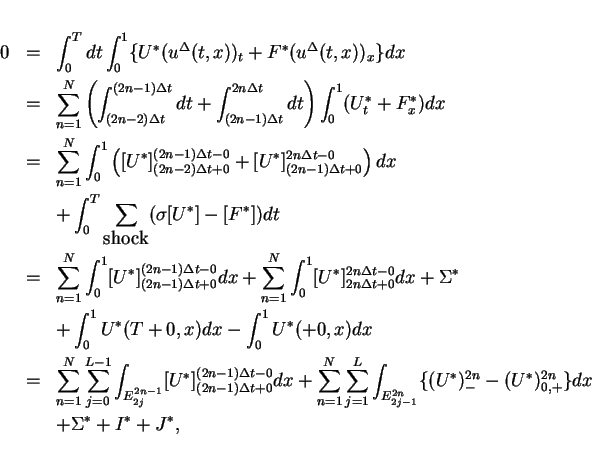
![\begin{eqnarray*}
J^\ast & = & \sum_{n=1}^N \sum_{j=1}^L \int_{E_{2j-1}^{2n}}
...
...\int_0^T \sum_{\mbox{shock}}
(\sigma [U^\ast]-[F^\ast]) dt,\\
\end{eqnarray*}](img181.gif)
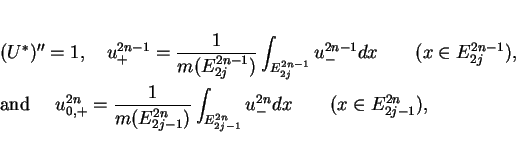
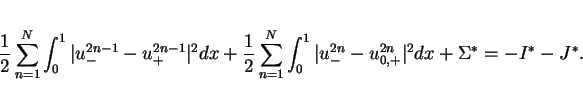
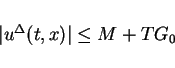
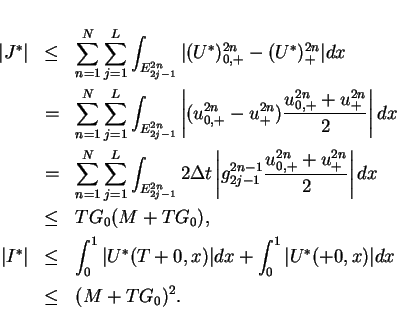
![]() be a function in
be a function in
![]() .
The integral
.
The integral
![\begin{eqnarray*}
\lefteqn{ \int\hspace{-6pt}\int _{[0,T]\times[0,1]}\{U(u^\Del...
...)_x\}dtdx \\
& = & \Sigma(\phi)+L_1(\phi)+L_2(\phi)+L_3(\phi),
\end{eqnarray*}](img199.gif)
![\begin{eqnarray*}
\Sigma(\phi) & = & \int_0^T \sum_{\mbox{shock}} (\sigma [U]-[...
...{2n}}
(\phi-\phi_{2j-1}^{2n})(U^{2n}_{-} - U^{2n}_{0,+})dx,\\
\end{eqnarray*}](img200.gif)
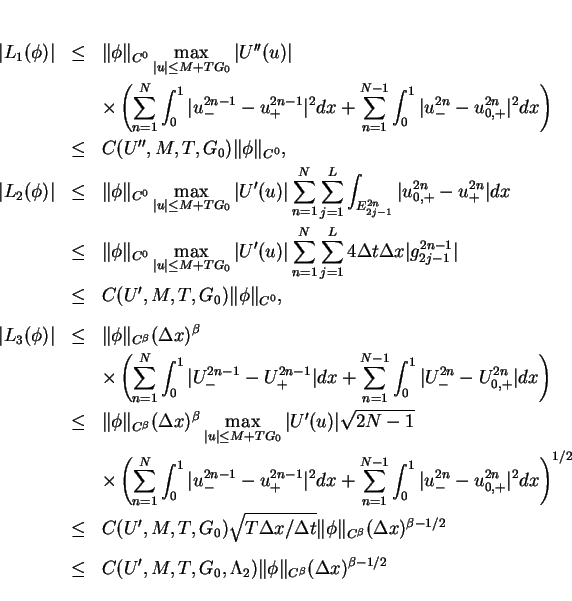
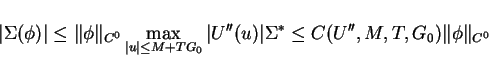
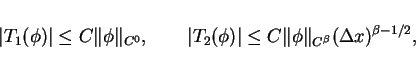
![]() (§4).
(§4).