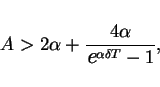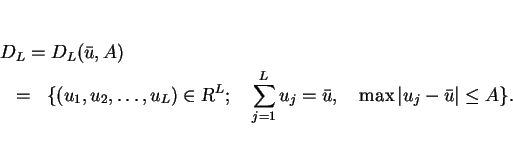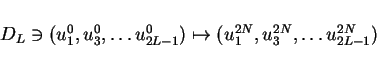

Next: 5 Compactness of entropy
Up: Time-periodic solutions
Previous: 3 Approximate Solution
(PDF file: paper9.pdf)
4 Decay estimates
In this section, we obtain the estimate for the approximation
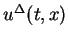 constructed in the last section by the similar way
to Tadmor ([13]) for fractional step Lax-Friedrichs
difference approximation.
constructed in the last section by the similar way
to Tadmor ([13]) for fractional step Lax-Friedrichs
difference approximation.
The step values
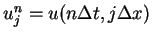 are able to be described
as forms of the Lax-Friedrichs difference scheme
are able to be described
as forms of the Lax-Friedrichs difference scheme
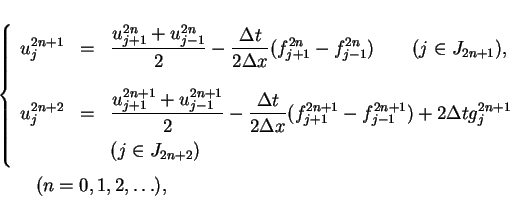 |
(18) |
where
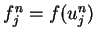 and
and
Let 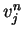 be the
be the 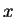 -backward difference of
-backward difference of 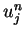
Then,
Similarly,
where 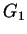 is the value in (15).
Let
is the value in (15).
Let
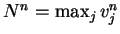 .
. 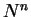 is non-negative because the summation
is non-negative because the summation
equals zero from the space periodicity of 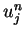 .
A function
.
A function
increases for
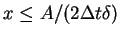 . Hence,
if
. Hence,
if
then
Similarly,
yields
The simple estimate for 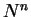
shows that if
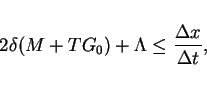 |
(19) |
then
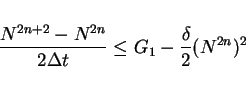 |
(20) |
for 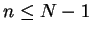 since
since
The solution 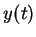 of ordinary differential equation
of ordinary differential equation
tends to the value
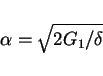 |
(21) |
as 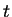 tends to infinity.
If
tends to infinity.
If 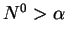 then
then 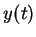 is monotone decreasing convex function,
and if
is monotone decreasing convex function,
and if 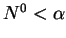 then
then 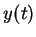 is monotone increasing concave one.
In the latter case, the tangent line of
is monotone increasing concave one.
In the latter case, the tangent line of 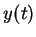 started
started 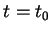 across the line
across the line 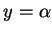 at
at
and the time is not smaller than
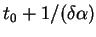 .
Hence, if
.
Hence, if
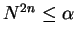 then
then
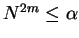 for
for
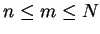 provided that
provided that
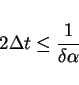 |
(22) |
from the inequality (20).
In the case 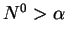 , it is easy to show that
, it is easy to show that
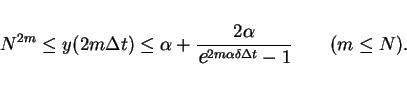 |
(23) |
We consider the estimate for 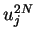 using above estimates
for
using above estimates
for 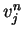 .
For the summation of
.
For the summation of 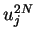
from (3).
Next simple lemma is used to the estimate for 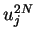 .
.
LEMMA 3
Let
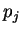
be real values which satisfy
and let
Then
The proof is omitted.
Let 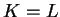 ,
,
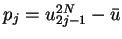 in Lemma
3, then
in Lemma
3, then
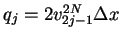 and
and
from (23).
Proposition 4 give the time-periodic
solution of the difference approximation.
Let 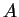 be sufficiently large number such that
be sufficiently large number such that
and let 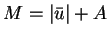 .
We take mesh lengths
.
We take mesh lengths 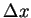 and
and 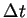 to satisfy
(19), (22) and
to satisfy
(19), (22) and
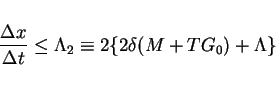 |
(25) |
for the estimation of the entropy (§5).
Let 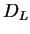 be a set
be a set
If we take
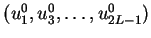 from
from 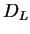 , set
, set
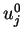 periodically for any
periodically for any 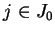 ,
then we can construct the approximation
,
then we can construct the approximation
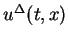 by the way
in §3.
Obviously
by the way
in §3.
Obviously 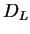 is a closed convex set and the range of the
mapping
is a closed convex set and the range of the
mapping
is contained in 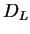 from Proposition 4.
Hence, we obtain the fixed point
from Proposition 4.
Hence, we obtain the fixed point
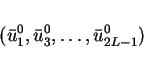 |
(26) |
of the mapping from Brouwer's fixed point theorem in 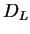 .
Of course, the fixed point depends on
.
Of course, the fixed point depends on  .
.


Next: 5 Compactness of entropy
Up: Time-periodic solutions
Previous: 3 Approximate Solution
Shigeharu TAKENO
15 January 2002
![]() constructed in the last section by the similar way
to Tadmor ([13]) for fractional step Lax-Friedrichs
difference approximation.
constructed in the last section by the similar way
to Tadmor ([13]) for fractional step Lax-Friedrichs
difference approximation.
![]() are able to be described
as forms of the Lax-Friedrichs difference scheme
are able to be described
as forms of the Lax-Friedrichs difference scheme
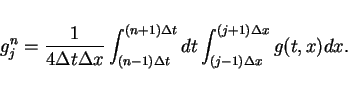
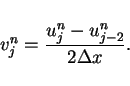
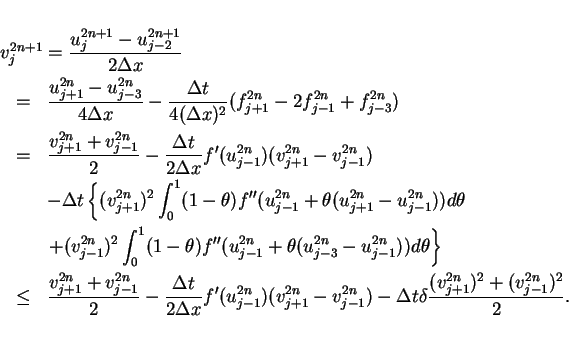
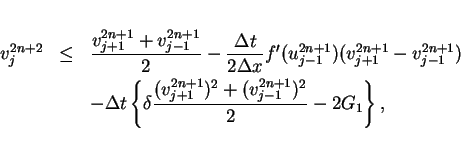
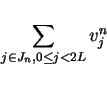
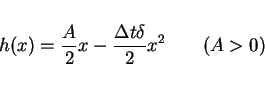
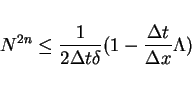
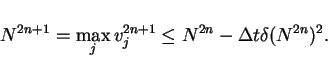
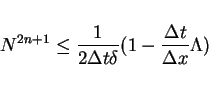
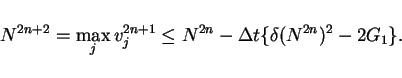
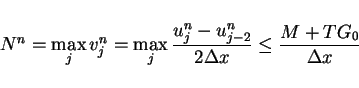
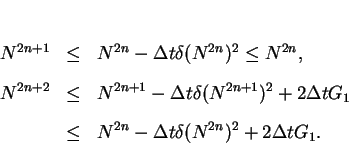
![]() of ordinary differential equation
of ordinary differential equation
![\begin{displaymath}
\left\{\begin{array}{l}
\displaystyle y'=G_1 - \frac{\delta}{2}y^2 [3ex]
y(0)=N^0\end{array}\right.\end{displaymath}](img136.gif)
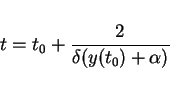
![]() using above estimates
for
using above estimates
for ![]() .
For the summation of
.
For the summation of ![]()
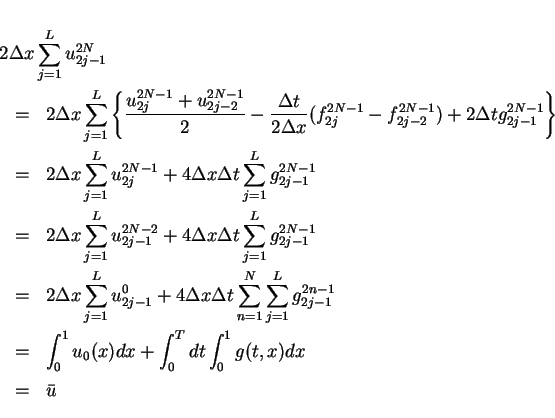
![]() .
.
![]() ,
,
![]() in Lemma
3, then
in Lemma
3, then
![]() and
and
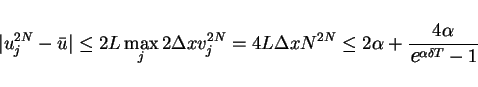
![]() be sufficiently large number such that
be sufficiently large number such that