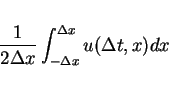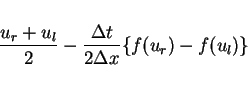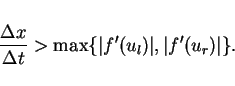

Next: 3 Approximate Solution
Up: Time-periodic solutions
Previous: 1 Introduction
(PDF file: paper9.pdf)
2 Preliminaries
A function 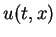 is called the weak solution of the
time-periodic problem (1) and
is called the weak solution of the
time-periodic problem (1) and
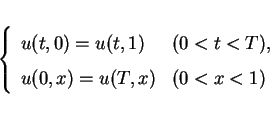 |
(7) |
with period 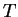 if the function
if the function 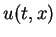 is bounded measurable in the region
is bounded measurable in the region
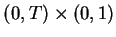 , and there exists a bounded measurable
function
, and there exists a bounded measurable
function 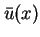 such that space-periodic extensions of
such that space-periodic extensions of
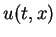 ,
, 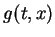 and
and 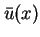 satisfy
satisfy
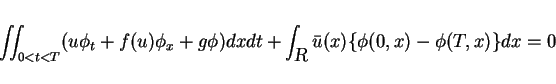 |
(8) |
for any
![$\phi(t,x) \in C^1_0([0,T]\times{\mbox{\sl R}}_x)$](img26.gif) .
.
Note that the definition has other equivalent forms.
One is the following:
![\begin{displaymath}
\displaystyle \int\hspace{-6pt}\int _{[0,T]\times[0,1]} (u\...
...\phi) dxdt
+ \int_0^1 \bar{u}(x)\{\phi(0,x)-\phi(T,x)\}dx = 0\end{displaymath}](img27.gif) |
(9) |
for any
![$\phi(t,x) \in C^1_0([0,T]\times[0,1])$](img28.gif) ,
,
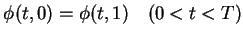 .
Another is expressed in terms of the space-periodic extension of
.
Another is expressed in terms of the space-periodic extension of
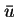 and for the
space and time periodic extension of
and for the
space and time periodic extension of 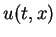 .
That is, it is required to satisfy
.
That is, it is required to satisfy
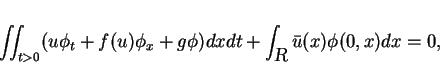 |
(10) |
for any
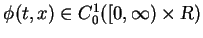 .
The conclusion is that
.
The conclusion is that 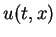 satisfies
(9) if and only if the followings valid
satisfies
(9) if and only if the followings valid
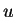 is solution of (1) in weak sense
is solution of (1) in weak sense
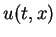 converges in weak sense to
converges in weak sense to 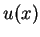 as
as 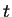 tends to
zero and as
tends to
zero and as 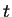 tends to
tends to 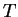
in 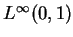 weak
weak .
.
-
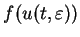 and
and
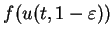 converge in weak sense
to the same value
converge in weak sense
to the same value
in 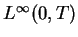 weak
weak for some function
for some function 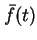 of
of
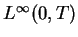 .
.
It seems that the function 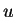 which satisfies above conditions
is a solution of the problem (1) satisfying
which satisfies above conditions
is a solution of the problem (1) satisfying
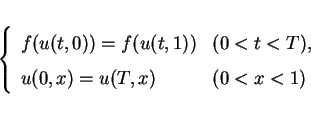 |
(11) |
instead of (7).
Certainly, both definitions are equivalent for the weak solution.
However, these include different means for the entropy condition.
The boundary condition of the original problem (7)
seems to say that the space-periodic extension satisfies the equation
(1), but the problem (11)
does not seem to require it. Hence in the case that boundary
values of the weak solution 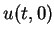 and
and 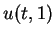 are different,
these should satisfy the entropy condition, that is,
are different,
these should satisfy the entropy condition, that is,
for (7), but should not
for (11).
It remains an open problem whether the boundary condition
(11) is well-posed.
A smooth function pair of 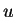
is an entropy pair for the scalar conservation law
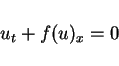 |
(12) |
if
for a smooth solution of (12).
This is equivalent that 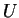 and
and 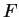 satisfy
satisfy
The function 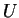 called entropy and
called entropy and 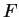 called entropy flux.
A weak solution
called entropy flux.
A weak solution 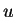 satisfies the entropy condition if
satisfies the entropy condition if
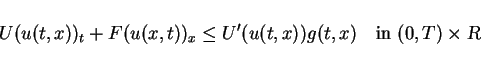 |
(13) |
for any smooth entropy pair with convex entropy 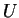 .
.
We suppose that the function 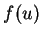 is smooth,
is smooth,
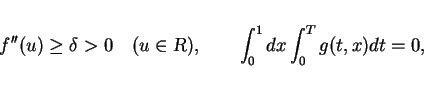 |
(14) |
and 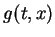 is a time-periodic function with period
is a time-periodic function with period 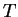 . The last
relation for
. The last
relation for 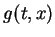 is need for the existence of a time periodic
solution.
is need for the existence of a time periodic
solution.
We also assume that the space-extension of 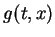 satisfies
satisfies
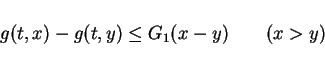 |
(15) |
for any 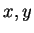 and
and  , where
, where 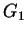 is a constant. The condition
is necessary by a technical reason.
is a constant. The condition
is necessary by a technical reason.
It is well-known that the solution of the Riemann problem
for the scalar conservation law
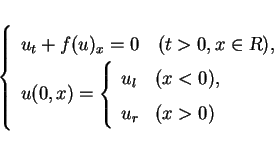 |
(16) |
is each of the two typical waves.
In the case 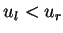 the solution is the rarefaction wave
the solution is the rarefaction wave
and in the case 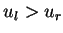 the solution is the shock wave
the solution is the shock wave
where the shock speed 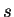 is determined by the
Rankine-Hugoniot relation
is determined by the
Rankine-Hugoniot relation
and Lax's entropy condition
(cf. [7], [12]).
We note that the average on the line 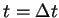
for the solution of the Riemann problem is equal to the
Lax-Friedrichs difference approximation
provided the Courant-Friedrichs-Lewy (CFL) condition


Next: 3 Approximate Solution
Up: Time-periodic solutions
Previous: 1 Introduction
Shigeharu TAKENO
15 January 2002
![]() is called the weak solution of the
time-periodic problem (1) and
is called the weak solution of the
time-periodic problem (1) and

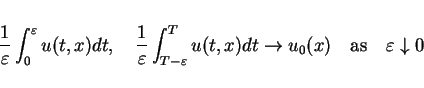
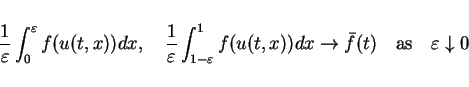
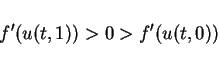
![]()
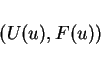
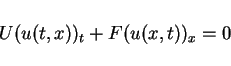
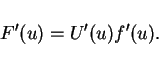
![]() is smooth,
is smooth,
![]() satisfies
satisfies
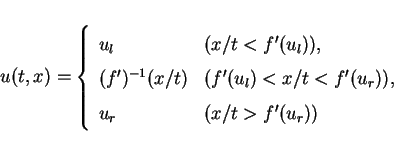
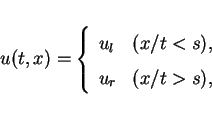
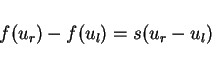
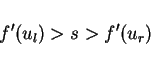
![]()