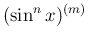
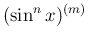 は、
[1] で見たように、以下のような形になる。
は、
[1] で見たように、以下のような形になる。
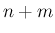 が奇数の場合は
が奇数の場合は 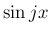 の線形結合で表される (
の線形結合で表される (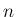 と
と 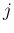 の偶・奇は一致する)
の偶・奇は一致する)
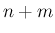 が偶数の場合は
が偶数の場合は 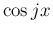 と 1 の線形結合で表される (
と 1 の線形結合で表される (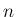 と
と 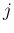 の偶・奇は一致する) が、
の偶・奇は一致する) が、
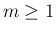 ならば 1 の線形結合は含まれない
ならば 1 の線形結合は含まれない
補題 1 により、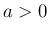 に対して、
に対して、
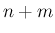 が奇数の場合は
が奇数の場合は 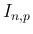 は収束し、
(19) でその値も計算でき、
は収束し、
(19) でその値も計算でき、
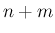 が偶数の場合は
が偶数の場合は 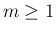 ならば収束して
(20) で計算できるが、
ならば収束して
(20) で計算できるが、
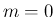 の場合、すなわち
の場合、すなわち 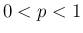 で
で 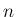 が偶数の場合は、
が偶数の場合は、
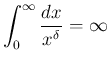
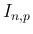 は発散することがわかる。
これで
は発散することがわかる。
これで 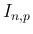 の収束性もわかったことになる。
すなわち、
の収束性もわかったことになる。
すなわち、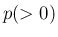 が非整数の場合、(3) の元、
が非整数の場合、(3) の元、
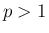 (
(![$m=[p]\geq 1$](img122.png) ) のときは
) のときは 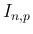 は収束、
は収束、
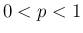 (
(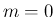 ) のときは、
) のときは、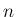 が奇数ならば収束するが、偶数ならば発散する。
が奇数ならば収束するが、偶数ならば発散する。
あとは、[1] と同様に 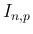 の値を計算する式を作ることにする。
[1] の計算により、以下がわかる (
の値を計算する式を作ることにする。
[1] の計算により、以下がわかる (![$\nu=[(n+1)/2]$](img123.png) ,
, ![$\mu=[(m+1)/2]$](img124.png) 、詳細は [1] を参照)。
、詳細は [1] を参照)。
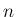 ,
, 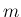 がいずれも奇数の場合は、
がいずれも奇数の場合は、
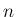 ,
, 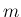 がいずれも偶数で
がいずれも偶数で 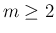 の場合は、
の場合は、
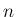 が奇数、
が奇数、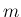 が偶数の場合は、
が偶数の場合は、
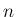 が偶数、
が偶数、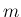 が奇数の場合は、
が奇数の場合は、
これを使うと、例えば 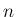 ,
, 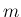 がともに奇数の場合は、
(18), (20), (21) より、
がともに奇数の場合は、
(18), (20), (21) より、
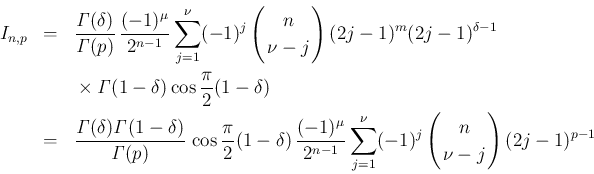
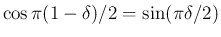 を用いると、
を用いると、
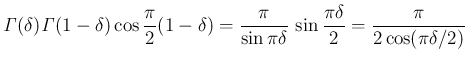
![$\nu=(n+1)/2 = [(n+1)/2]$](img140.png) であり、
であり、
![$m=[p]$](img141.png) (
(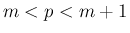 ) は奇数なので、
) は奇数なので、
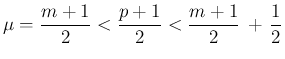
![$\mu = [(p+1)/2]$](img144.png) と書ける。
と書ける。
また、すべての自然数 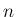 と実数
と実数 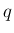 に対して
に対して 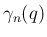 を、
を、
![$\nu=[(n+1)/2]$](img123.png) として
として
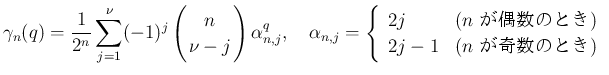
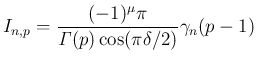
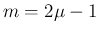 なので、
なので、
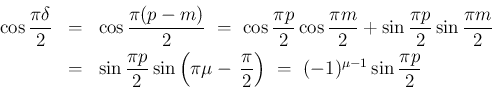
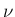 ,
, 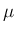 ,
, 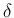 ,
, 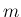 を用いない形に表すこともできる。
を用いない形に表すこともできる。
以下、他の場合も同様に変形を行う。
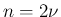 ,
, 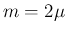 の場合は、(18), (20), (22) より、
の場合は、(18), (20), (22) より、
![\begin{eqnarray*}I_{n,p}
&=& \frac{\mathit{\Gamma}(\delta)}{\mathit{\Gamma}(p)}...
.../2)}\gamma_{n}(p-1)
\hspace{1zw}\hspace{1zw}(\nu=n/2=[(n+1)/2]) \end{eqnarray*}](img157.png)
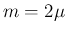 より、
より、
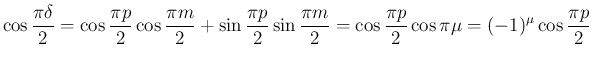
![\begin{eqnarray*}I_{n,p}
&=& \frac{\mathit{\Gamma}(\delta)}{\mathit{\Gamma}(p)}...
...\gamma_{n}(p-1)
\hspace{1zw}\hspace{1zw}(\nu=(n+1)/2=[(n+1)/2]) \end{eqnarray*}](img161.png)
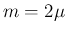 より、
より、
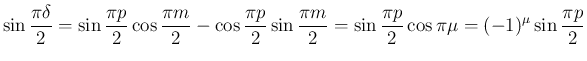
最後に 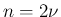 ,
, 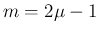 の場合は、(18), (19), (24) より、
の場合は、(18), (19), (24) より、
![\begin{eqnarray*}I_{n,p}
&=& \frac{\mathit{\Gamma}(\delta)}{\mathit{\Gamma}(p)}...
.../2)}\gamma_{n}(p-1)
\hspace{1zw}\hspace{1zw}(\nu=n/2=[(n+1)/2]) \end{eqnarray*}](img157.png)
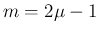 より、
より、
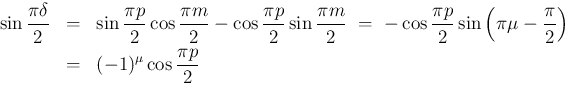
![$m=[p]$](img141.png) の偶・奇に関わらない形に書けることになる。
の偶・奇に関わらない形に書けることになる。
竹野茂治@新潟工科大学