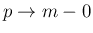
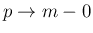 への極限について考察しておく。
への極限について考察しておく。
最終的な形 (31) には、ガンマ関数は含まれるものの、
あとは 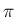 と三角関数と有理数と整数の
と三角関数と有理数と整数の 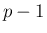 乗だけなので、
[1] の
乗だけなので、
[1] の 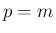 の場合の対数が現れる式とは
かなり違うように見える。
実際に
の場合の対数が現れる式とは
かなり違うように見える。
実際に
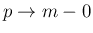 としたときに、
としたときに、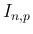 の極限が [1] で得られたものになるのかどうかをここで見ておく。
の極限が [1] で得られたものになるのかどうかをここで見ておく。
まず、(31) には 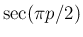 や
や
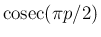 が
含まれているので、
が
含まれているので、
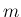 の偶・奇によって極限の特異性がそこに現れる。すなわち、
の偶・奇によって極限の特異性がそこに現れる。すなわち、
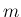 が奇数なら
が奇数なら
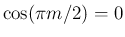 だから
だから 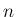 が偶数であれば sec の部分が発散し、
が偶数であれば sec の部分が発散し、
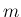 が偶数なら、
が偶数なら、
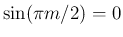 だから
だから 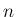 が奇数であれば cosec の部分が発散する。
逆に特異性が現れないのは、
が奇数であれば cosec の部分が発散する。
逆に特異性が現れないのは、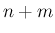 が偶数のときということになる。
が偶数のときということになる。
![$\mu=[(m+1)/2]$](img124.png) とすると、
とすると、
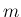 が奇数の場合は、
が奇数の場合は、
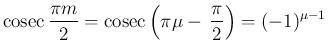
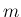 が偶数の場合は、
が偶数の場合は、
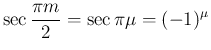
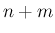 が偶数 (
が偶数 (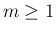 ) の場合は
いずれも (31) より、
) の場合は
いずれも (31) より、
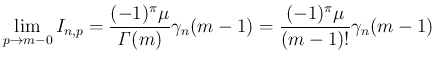
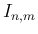 の式に一致する
ことがわかる。
の式に一致する
ことがわかる。
問題は、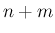 が奇数の場合であるが、
この場合は、[1] の (26), (32) により
が奇数の場合であるが、
この場合は、[1] の (26), (32) により
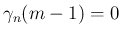 で
あることがわかる。それにより
で
あることがわかる。それにより 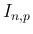 の sec, cosec の特異性が解消
されることになる。
の sec, cosec の特異性が解消
されることになる。
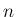 が奇数で
が奇数で 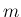 が偶数 (
が偶数 (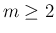 ) の場合は、(31)、
およびロピタルの定理により、
) の場合は、(31)、
およびロピタルの定理により、
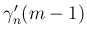 は、
は、
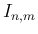 の式が得られることがわかる。
すなわちこの log は、
の式が得られることがわかる。
すなわちこの log は、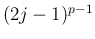 の
の 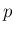 に関する導関数の計算から
でてくることになるし、
に関する導関数の計算から
でてくることになるし、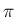 が消える理由も分母の
が消える理由も分母の 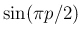 の
微分によることがわかる。
の
微分によることがわかる。
同様に、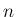 が偶数で
が偶数で 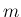 が奇数の場合も、(31)、
およびロピタルの定理により、
が奇数の場合も、(31)、
およびロピタルの定理により、
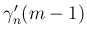 は、
は、
竹野茂治@新潟工科大学