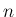
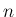 が奇数で、
が奇数で、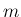 が偶数の場合を考える。
が偶数の場合を考える。
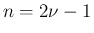 ,
, 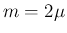 とすると、
とすると、
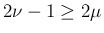 より
より
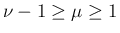 となる。
となる。
(5) より、
であり、補題 2, 3 より、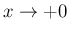 で
で
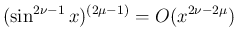
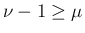 より (31) で
より (31) で 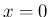 とすると、
となり、(31) の
とすると、
となり、(31) の 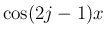 の係数の和が 0 となる。
よって補題 1 と (30),
(31) より
となる (
の係数の和が 0 となる。
よって補題 1 と (30),
(31) より
となる (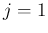 は
は 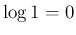 により消える)。
元の
により消える)。
元の 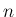 ,
, 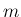 で表すと、(33) は、
で表すと、(33) は、
以上の 4 つの式 (19), (23), (29), (34) には共通部分もあるので、 以下のようにまとめることもできる。
ここで、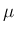 ,
, 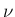 は
は
![$\mu = [(m+1)/2]$](img143.png) ,
, ![$\nu=[(n+1)/2]$](img144.png) (
(![$[\ ]$](img145.png) はガウス記号)、
はガウス記号)、
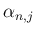 ,
, 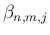 は以下の通り。
は以下の通り。
