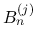
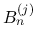 ,
, 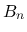 の評価には, 以下の補題を用いる.
の評価には, 以下の補題を用いる.
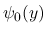 に対して
に対して
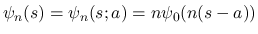 とすると, 任意の有限区間
とすると, 任意の有限区間 ![$I=[p,q]$](img205.png) に対して次が成り立つ.
に対して次が成り立つ.
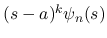
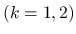 は
は 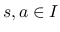 ,
, 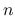 に関して有界で,
に関して有界で, 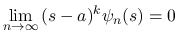
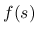 が
が 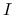 上連続ならば,
上連続ならば, 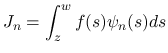
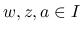 (
(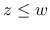 ),
), 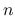 に関して有界で, 以下が成り立つ.
に関して有界で, 以下が成り立つ.
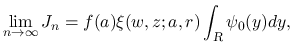
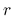 ,
, 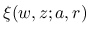 は,
は, 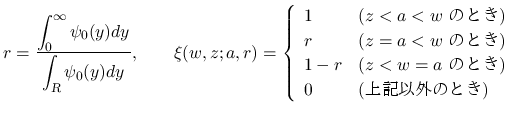
補題 3 の証明
1. 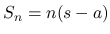 とすると,
とすると,
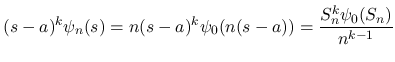
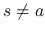 であれば (16) により 0 に収束し,
であれば (16) により 0 に収束し, 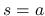 のときは
のときは 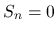 より 0 となる.
より 0 となる.
2. 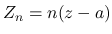 ,
, 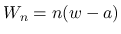 とすると,
とすると,
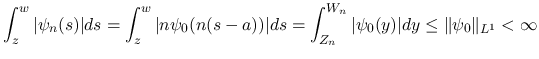
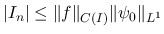
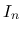 は一様有界となる.
は一様有界となる.
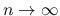 に対しては,
に対しては, 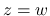 なら
なら 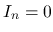 ,
, 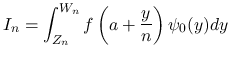
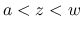 ならば
ならば
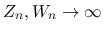 ,
, 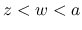 ならば
ならば
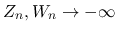 となるので これらの場合は
となるので これらの場合は
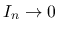 となる.
となる.
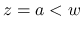 の場合は,
の場合は, 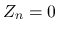 ,
,
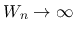 となるので,
となるので,
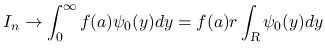
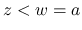 のときは,
のときは,
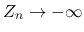 ,
, 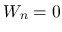 より
より
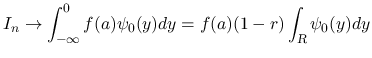
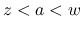 のときは,
のときは,
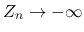 ,
,
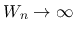 より
より
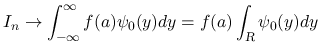
次は, この補題 3 を用いて, 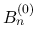 ,
, 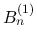 の
評価を行う. まずは
の
評価を行う. まずは 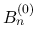 から.
から.
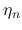 ,
, 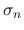 は,
は, 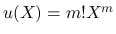 とすると, (20), (21) と, 境界値 (19) により,
とすると, (20), (21) と, 境界値 (19) により,
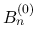 は
は
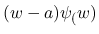 ,
,
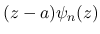 は
は
![$w,z,a\in [z_1,w_1]$](img259.png) で有界で,
で有界で,
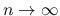 のときに 0 に収束する. 積分項も有界で,
のときに 0 に収束する. 積分項も有界で,
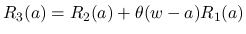 とすると
に収束するから, 結局
とすると
に収束するから, 結局 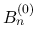 は有界で, (28) に収束することがわかる.
は有界で, (28) に収束することがわかる.
次に 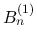 は,
は,
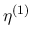 は
は ![$[z_1,w_1]$](img268.png) 上有界なので, この 3 行の式のうち, 最初の行は
上有界なので, この 3 行の式のうち, 最初の行は 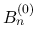 の場合と同様に有界で 0 に収束する.
2 行目の式は,
の場合と同様に有界で 0 に収束する.
2 行目の式は, 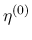 に
に 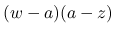 が含まれているので, これもやはり
が含まれているので, これもやはり 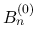 の場合と同様に有界で 0 に収束する.
3 行目の 2 つの積分項も有界で,
に収束するから, 結局
の場合と同様に有界で 0 に収束する.
3 行目の 2 つの積分項も有界で,
に収束するから, 結局 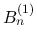 は有界で (30) に
収束する.
は有界で (30) に
収束する.
よって, Lebesgue 収束定理により, 以下がわかる.
ここから,
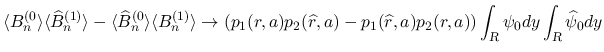
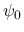 ,
,
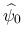 が
を満たせば,
が
を満たせば, 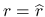 となり, よって,
となる. これと, (25) を組み合わせると, 以下が得られる.
となり, よって,
となる. これと, (25) を組み合わせると, 以下が得られる.
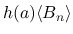 は
は ![$a\in[z_1,w_1]$](img278.png) に関して有界で,
に関して有界で, 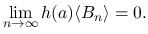
竹野茂治@新潟工科大学