9 いくつかの証明
この節では、いくつかの命題の証明を紹介する。
まず、命題 1 を証明する。
それには、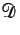 は
は 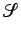 で稠密なので、
で稠密なので、
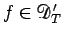 に対し、
ある自然数
に対し、
ある自然数 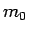 とある正数
とある正数 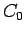 があり、
があり、
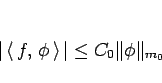 |
(22) |
がすべての
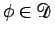 に対して成り立つことを示せばよい。
に対して成り立つことを示せばよい。
まず、4 節の 1 の分割 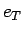 に対し、
に対し、
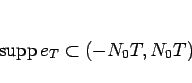
となる自然数 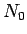 を取る。
を取る。
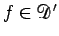 であるから、
この
であるから、
この 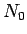 に対し、ある自然数
に対し、ある自然数 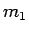 と正数
と正数 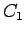 があり、
任意の
があり、
任意の
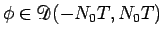 に対して
に対して
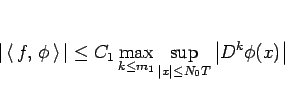 |
(23) |
とできる。なお、この 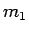 は、必要ならば取り直して 2 以上
であるとしてよい。
は、必要ならば取り直して 2 以上
であるとしてよい。
さて、任意の
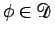 に対し、
命題 2 により
に対し、
命題 2 により
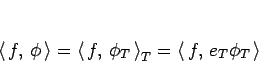 |
(24) |
であり、
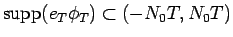 であるから、
(23) より
であるから、
(23) より
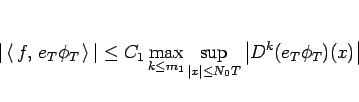 |
(25) |
とできる。ここで、
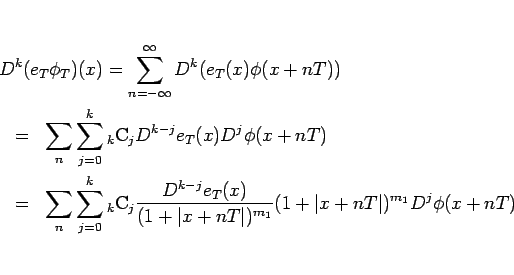
とすると、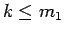 より
より
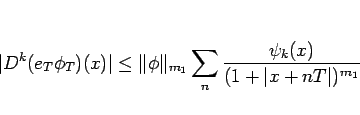 |
(26) |
となることがわかる。ここで、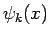 は
は
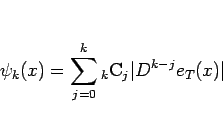
としたが、これは
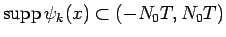 で非負の
有界な関数である。
で非負の
有界な関数である。
(24), (25), (26) を合わせると結局
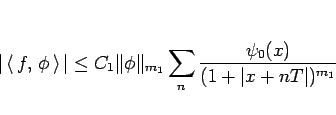 |
(27) |
となる。ここで、
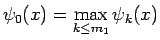 とした。
(27) の
とした。
(27) の 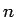 に関する和の部分を、
に関する和の部分を、
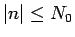 に対するものと、
に対するものと、
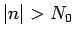 に関するものに分けると、
に関するものに分けると、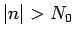 のときは
のときは 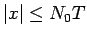 より
より
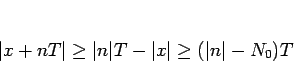
なので、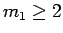 より、
より、
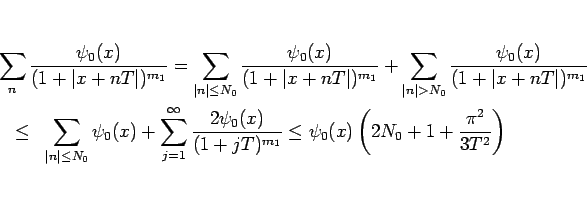
でおさえられる。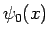 は有界なので、
これで (22) が成り立つこと (
は有界なので、
これで (22) が成り立つこと (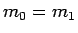 ) が示された。
) が示された。
次は、命題 8 を示す。それには、次のベッセルの不等式を用いる。
命題 12
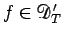 が
が 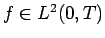 ならば、
すべての
ならば、
すべての 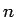 について次が成り立つ。
について次が成り立つ。
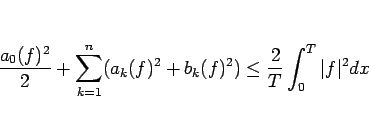 |
(28) |
証明
不等式 (28) の左辺を 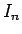 とすると、
フーリエ級数の部分和
とすると、
フーリエ級数の部分和 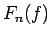 ((14)) は、
((14)) は、
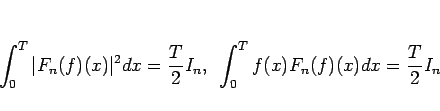
となり (計算は略)、よって
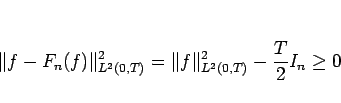
となるので、
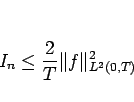
が言える。
命題 8 の証明に戻る。
今、
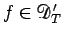 が
が 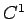 級である場合は
級である場合は
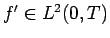 なので、
これにベッセルの不等式を適用すると、
なので、
これにベッセルの不等式を適用すると、
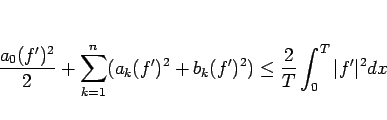
となるが、補題 7 よりこれは
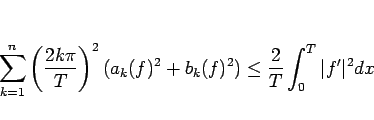 |
(29) |
を意味する。よって、
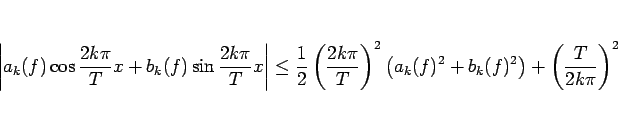
より、(29) によりこの右辺の和が
 に対する収束する優級数を作るので、
結局
に対する収束する優級数を作るので、
結局  が一様収束することになる。
が一様収束することになる。
最後は命題 11。
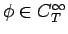 とすると、
とすると、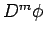 にベッセルの不等式を適用すれば、
(11) と同様にして
にベッセルの不等式を適用すれば、
(11) と同様にして
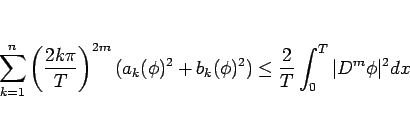 |
(30) |
が得られ、左辺は
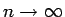 のときに
右辺でおさえられて有界なので、
のときに
右辺でおさえられて有界なので、
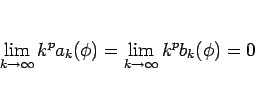
が 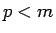 に対して言えることになる。
に対して言えることになる。 はいくらでも大きくとれるので、
これで命題 11 も成り立つことが示された。
はいくらでも大きくとれるので、
これで命題 11 も成り立つことが示された。
竹野茂治@新潟工科大学
2015年6月1日
![]() は
は ![]() で稠密なので、
で稠密なので、
![]() に対し、
ある自然数
に対し、
ある自然数 ![]() とある正数
とある正数 ![]() があり、
があり、
![]() に対し、
に対し、
![]() に対し、
命題 2 により
に対し、
命題 2 により
![]() が
が ![]() ならば、
すべての
ならば、
すべての ![]() について次が成り立つ。
について次が成り立つ。
![]() とすると、
フーリエ級数の部分和
とすると、
フーリエ級数の部分和 ![]() ((14)) は、
((14)) は、
![]() が
が ![]() 級である場合は
級である場合は
![]() なので、
これにベッセルの不等式を適用すると、
なので、
これにベッセルの不等式を適用すると、
![]() とすると、
とすると、![]() にベッセルの不等式を適用すれば、
(11) と同様にして
にベッセルの不等式を適用すれば、
(11) と同様にして