![]() に対するフーリエ級数の部分和
に対するフーリエ級数の部分和
(14)
本節では、この定理の証明を紹介する。
任意の
![]() ,
,
![]() に対し、
に対し、
![]() で、次が成り立つ。
で、次が成り立つ。
証明
![]() となることは容易にわかる。
まず 1. から考える
となることは容易にわかる。
まず 1. から考える
また、2. の方は 1. より、
任意の
![]() に対し、
に対し、
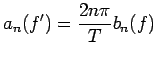 ,
,
 ,
,
![]() .
.
証明
補題 6 より、
さて、定理 5 は、任意の
![]() に対して、
に対して、
さて、次は良く知られている。
![]() が
が ![]() 級 (
級 (![]() ,
, ![]() が連続) であれば、
が連続) であれば、
![]() は
は ![]() に一様収束する。
に一様収束する。
この証明は 9 節で紹介する。
この命題 8 により、![]() は
は ![]() に
一様収束することがわかるが、補題 7 より
に
一様収束することがわかるが、補題 7 より
![]() であり、
これも命題 8 により
であり、
これも命題 8 により ![]() に一様収束することになる。
これにより、
に一様収束することになる。
これにより、
![]() は、
は、
![]() で
で ![]() に収束することがわかる。
実際、
に収束することがわかる。
実際、
![]() のサポートは
のサポートは ![]() にかかわらず
にかかわらず ![]() の
サポートに含まれ、
の
サポートに含まれ、
よって、
![]() は
は
![]() に収束し、
結局、
に収束し、
結局、
つまり、周期超関数のフーリエ級数の収束は、
テスト関数のフーリエ級数の収束に帰着されて示されることになる。
なお、この定理 5 により、
(13) も ![]() (
(
![]() ) では等号になる。
) では等号になる。
竹野茂治@新潟工科大学