まず次の補題を示す。
![]() 行列
行列 ![]() ,
,
![]() に対し、
に対し、
証明
行列 ![]() を
を
![\begin{displaymath}
A
=
\left[\begin{array}{c}\alpha_1\\ \alpha_2\\ \vdots \\...
... \vdots \\ \alpha_N\end{array}\right]
=
A_1+A_2+\cdots +A_N
\end{displaymath}](img1519.png)
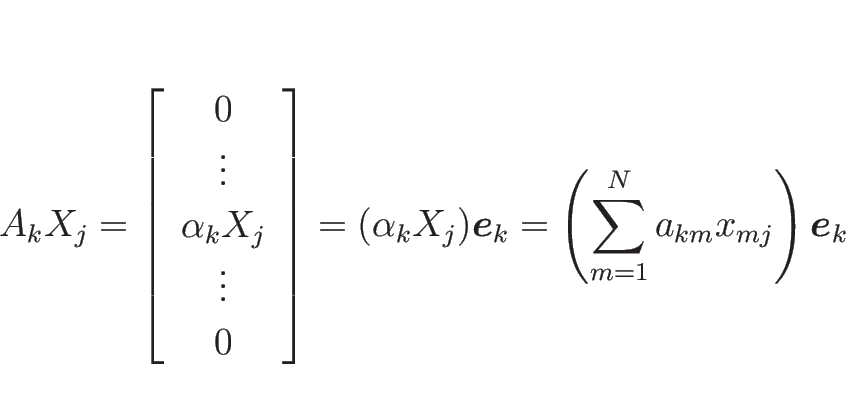
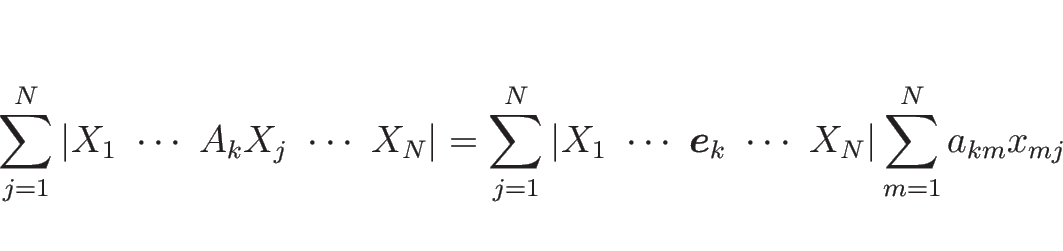
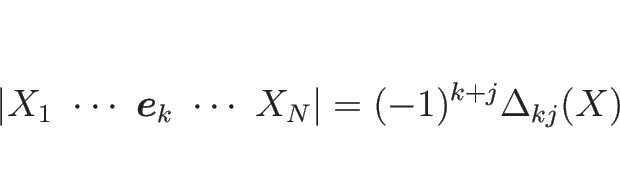
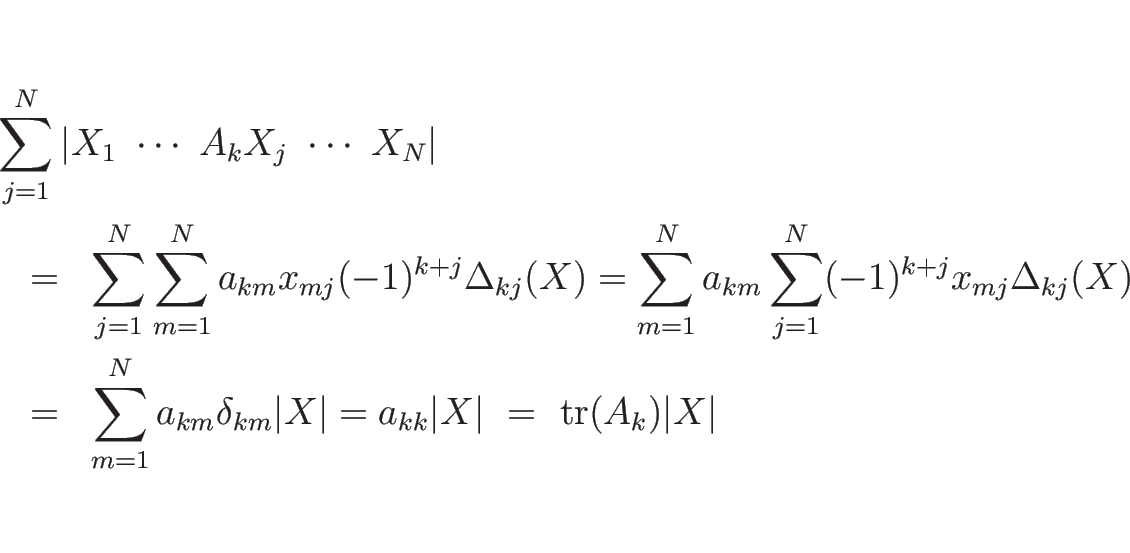
![]() が
が ![]() 内で滑らかで、かつ 0 ではないベクトルであるとき、
内で滑らかで、かつ 0 ではないベクトルであるとき、
![]() 内の各点
内の各点 ![]() に対して、そのある近傍
に対して、そのある近傍 ![]() (
(
![]() )、
および
)、
および ![]() の原点のある近傍
の原点のある近傍
![]() と
その上のベクトル値関数
と
その上のベクトル値関数
![]() を、
を、
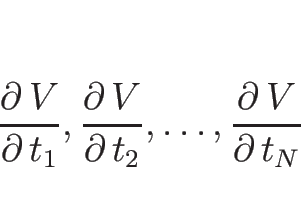
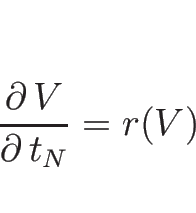
証明
このような関数の存在は、通常の常微分方程式の理論から得られる。
まず、![]() 内に、
内に、![]() を通り、
を通り、
![]() のある近傍
のある近傍 ![]() (
(
![]() ) では
) では ![]() とは接しない
とは接しない ![]() 次元の滑らかな初期面
次元の滑らかな初期面
(C.15) が ![]() で
で ![]() 次元の
初期面を構成することから、
次元の
初期面を構成することから、![]() は
は ![]() 次元空間の
原点を含むある開集合
次元空間の
原点を含むある開集合
![]() から
から ![]() への滑らかな写像で、
への滑らかな写像で、![]() の
の ![]() 個の接ベクトル
個の接ベクトル
![]() は
は ![]() 上
一次独立でなくてはならない。
さらに、
上
一次独立でなくてはならない。
さらに、![]() は
は ![]() とは接しないので、
とは接しないので、
![]() に対して、
に対して、
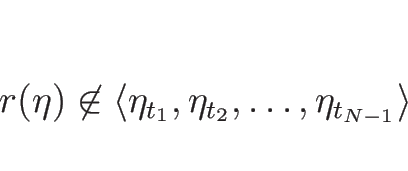
例えば、上の超平面は、
![]() より、
より、
![]() の 0 でない成分で割ることで
の 0 でない成分で割ることで ![]() を
を ![]() 個の
パラメータで表せる。簡単のため、
個の
パラメータで表せる。簡単のため、![]() の
の ![]() 番目の成分が 0 でないとすると、
番目の成分が 0 でないとすると、
![\begin{displaymath}
\eta = \left[\begin{array}{c} u^1_1+t_1\\ u^1_2+t_2\\ \vdot...
...\\ u^1_N\end{array}\right],
\hspace{0.5zw}a_N\neq 0
\right)
\end{displaymath}](img1538.png)
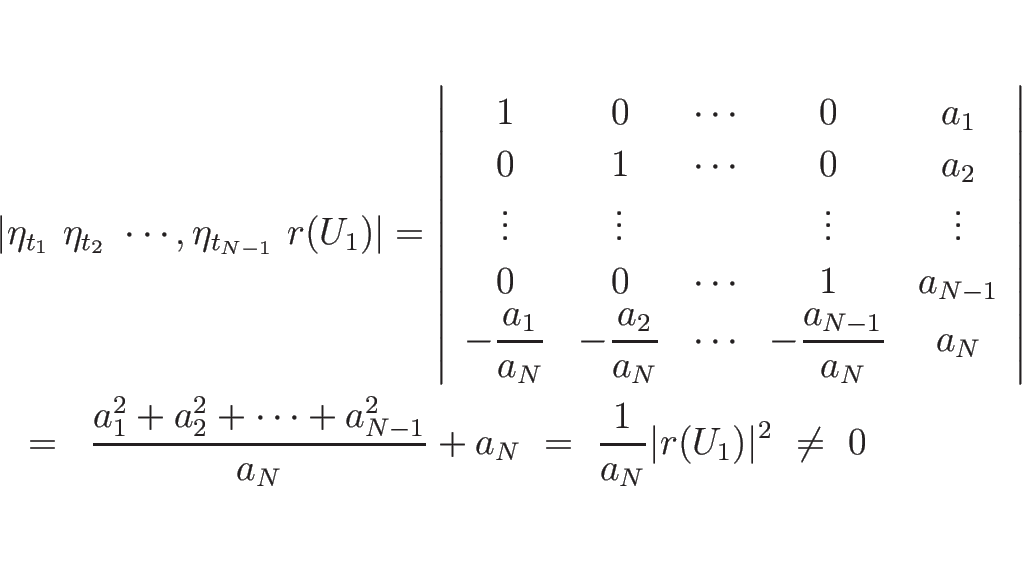
これに対して、常微分方程式の初期値問題
常微分方程式の一般論と ![]() ,
, ![]() の滑らかさより、
の滑らかさより、
![]() のある近傍に対して
この解
のある近傍に対して
この解 ![]() が存在し、
が存在し、
![]() に関して滑らかで
あることが示され、
に関して滑らかで
あることが示され、
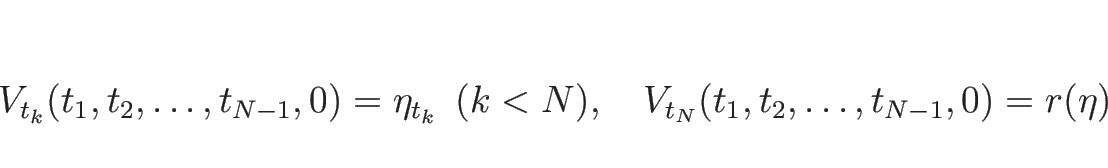
なお、当初は、
この補題 C.2 の証明をさらに
以下のように続けて、
補題 C.1 を用いることで ![]() 内で大域的に
内で大域的に ![]() が存在することを示そうとしていた。
が存在することを示そうとしていた。
(当初証明の続きとしていたもの)
のときに
のヤコビ行列式が (C.18) に より 0 ではないので、
が十分小さければ (C.19) となる。 さらにこの行列式は、微分方程式 (C.17) の解が 存在し続ける間の
すべてに対して 0 ではないことを示す。 (C.19) の左辺のヤコビ行列式を
とする:
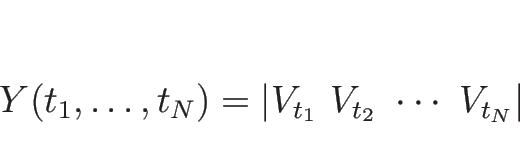
仮定よりであり、 この
を
で微分すると、
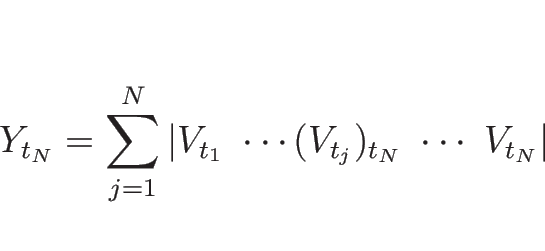
となり、
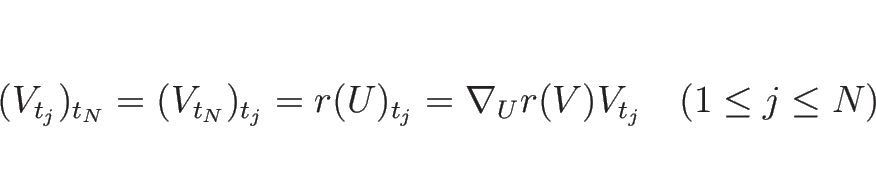
より、補題 C.1 から
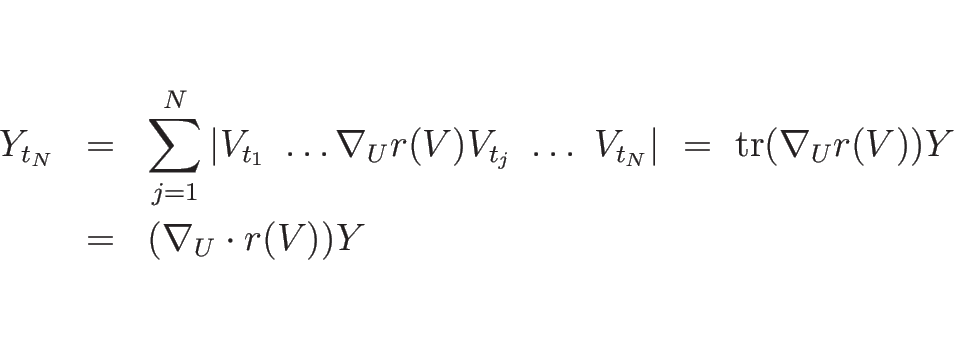
となる (は
の発散)。 よって、これを
に関する微分方程式と見れば、その解は
と書け、これは、確かにで、また
は
上で滑らかなので、 この式 (C.20) より 解
が存在している
に対して
は 0 に なることはない。
初期面 ![]() の取り方によってはその流管は
の取り方によってはその流管は ![]() 全体を
渡らないこともあるし、どのような
全体を
渡らないこともあるし、どのような ![]() に対しても、
流管が
に対しても、
流管が ![]() 全体となり
全体となり ![]() に接しないような
初期面を取ることが可能かといえば、それは自明ではない。
だから、補題 C.2 を
に接しないような
初期面を取ることが可能かといえば、それは自明ではない。
だから、補題 C.2 を ![]() 全体に渡るような解の存在という形で述べることは難しい。
全体に渡るような解の存在という形で述べることは難しい。
次は、命題 3.1 の 1. の証明を行う。 これも、当初の大域的な形から、現在は局所的な形に直してある。
証明
補題 C.2 の
![]() と近傍
と近傍 ![]() ,
, ![]() は、
は、
![]() の上でヤコビ行列式
の上でヤコビ行列式 ![]() が 0 ではないので、
必要ならばさらに小さい近傍を取ることで、
逆関数定理より
が 0 ではないので、
必要ならばさらに小さい近傍を取ることで、
逆関数定理より
![]() と
と ![]() が 1 対 1 に対応するようにでき、
各
が 1 対 1 に対応するようにでき、
各 ![]() を
を ![]() の滑らかな関数
の滑らかな関数 ![]() と表せる。
と表せる。
この ![]() は、
は、
![]() を満たすので、
を満たすので、
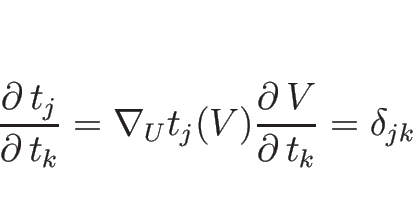
![\begin{displaymath}
\left[\begin{array}{c}\nabla_U t_1(V)\\ \vdots\\ \nabla_U t...
... t_1}\ \cdots\ \frac{\partial\, V}{\partial\, t_N}\right] = E
\end{displaymath}](img1571.png)
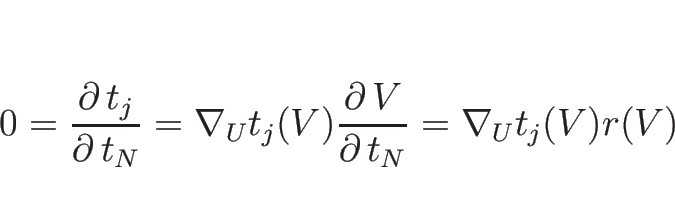
また、この証明の逆関数定理を使用する部分も、
当初は「ヤコビ行列式が 0 でない範囲で逆関数が求まる」
ように書いていたが、それは正しくなく、
「ある点でヤコビ行列式が 0 でない場合その近傍で逆関数が求まる」
と、あくまで局所的な形でなければいけない。
証明
上の証明にあるように、![]() として
として ![]() (
(![]() ) を取れば
もちろんであるが、命題 3.1 の
条件を満たす一般の
) を取れば
もちろんであるが、命題 3.1 の
条件を満たす一般の ![]() に対しても、
それに対して上の証明の
に対しても、
それに対して上の証明の ![]() を
を ![]() とすると、
とすると、
![]() は
は
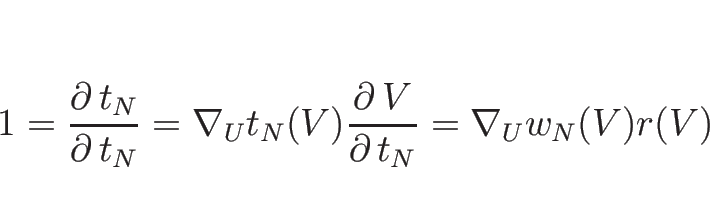
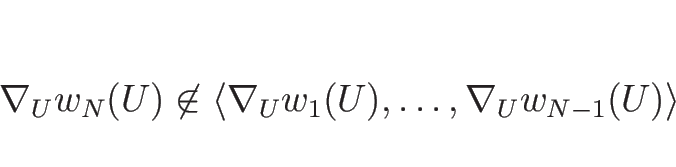
今、命題 3.1 の
2. の条件を満たす
![]() に
に
![]() を代入すれば、
を代入すれば、
![]() は
は ![]() ,...,
,...,![]() の関数と見ることができるが、
の関数と見ることができるが、
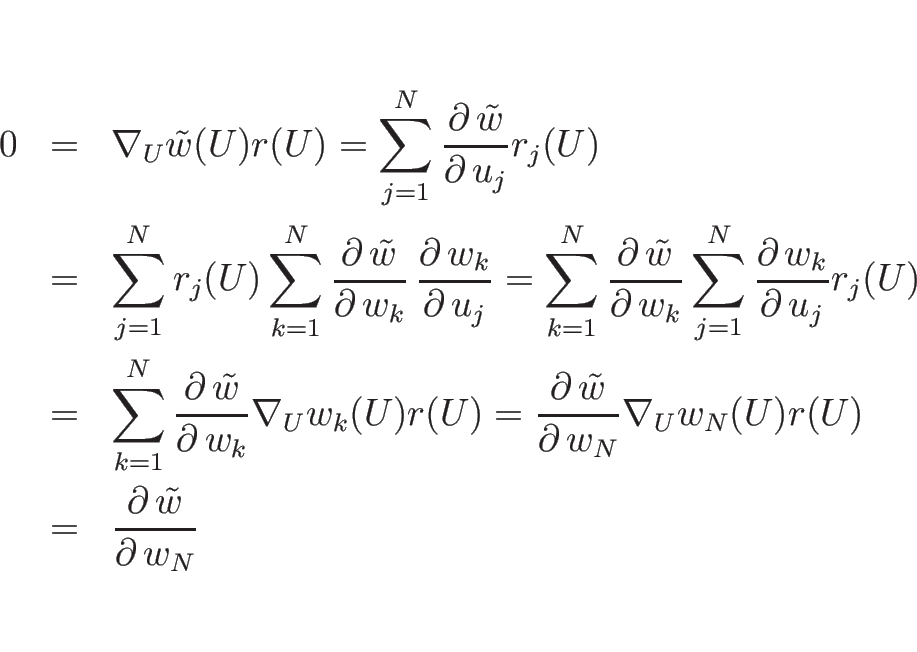
この証明も、前の証明同様逆関数の定理を使用している部分は、
局所的にしか言えないので、その範囲に制限して成り立つことになる。
つまり、命題 3.1 の最初の ![]() は、
1. と 2. の証明の両方の「近傍」の
共通部分として得られる小さい近傍ということになる。
は、
1. と 2. の証明の両方の「近傍」の
共通部分として得られる小さい近傍ということになる。
もちろん、個々の保存則方程式の具体例に関しては、
リーマン不変量が ![]() の定義域全体で存在することも多いし、
この命題 3.1 の証明でも
の定義域全体で存在することも多いし、
この命題 3.1 の証明でも ![]() が「保存則方程式の固有ベクトル」であることは
特に使用していないので、
もしかしたら
が「保存則方程式の固有ベクトル」であることは
特に使用していないので、
もしかしたら ![]() が保存則方程式の固有ベクトルの場合には
もう少し大域的な結果が成立する可能性はなくはない。
しかしそれは当然自明ではないので、
とりあえず一般論としては局所的なものに留めておくべきであろう。
が保存則方程式の固有ベクトルの場合には
もう少し大域的な結果が成立する可能性はなくはない。
しかしそれは当然自明ではないので、
とりあえず一般論としては局所的なものに留めておくべきであろう。
竹野茂治@新潟工科大学