しかし、![]() 全体で滑らかなものが取れかどうかは自明ではなく、
全体で滑らかなものが取れかどうかは自明ではなく、
![]() や
や ![]() の形状によっては怪しい場合もでてくるので、
本節ではそれを少し細かく考えることにする。
の形状によっては怪しい場合もでてくるので、
本節ではそれを少し細かく考えることにする。
なお、保存則方程式の解として「小さい解」、
すなわち初期値のすべての値がある定ベクトルの近くにあり、
変動が小さく、それに対する方程式の解もその近くだけに留まるものだけを
考えるような局所的な立場では、
局所的に滑らかな固有値、固有ベクトルが取れることは言えるので、
3.2 節の最後に
「なお」として追記したように、必要ならば ![]() を狭く取ることで、
を狭く取ることで、
![]() 全体で滑らかなものが存在する、とすることができる。
本節では、局所的とは限らない立場も含めて考察する。
全体で滑らかなものが存在する、とすることができる。
本節では、局所的とは限らない立場も含めて考察する。
まず、固有値 ![]() が
が ![]() 全体で滑らかに取れるかどうかを考える。
仮定として、
全体で滑らかに取れるかどうかを考える。
仮定として、![]() は
は ![]() 上の領域、すなわち連結開集合であるとし、
上の領域、すなわち連結開集合であるとし、
![]() は
は ![]() 上で滑らかな関数 (例えば
上で滑らかな関数 (例えば
![]() ) で、
) で、
![]() 上で双曲型、すなわち
上で双曲型、すなわち ![]() が
が ![]() 上で異なる
上で異なる ![]() 個の実固有値
個の実固有値
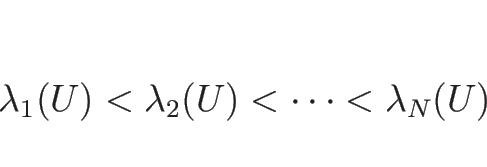
![]() は、
は、![]() の成分の多項式を係数とする
の成分の多項式を係数とする ![]() の
の ![]() 次方程式
次方程式
![]() は、方程式 (C.1) を
満たすが、この方程式は重解を持たないので、
は、方程式 (C.1) を
満たすが、この方程式は重解を持たないので、
![]() に対し、
に対し、
![]() であるが、
(C.2) から陰関数定理により、
であるが、
(C.2) から陰関数定理により、
![]() のある近傍で
のある近傍で ![]() は滑らかで、
は滑らかで、
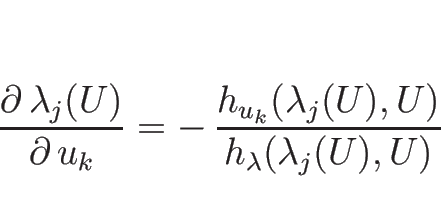
しかし、固有ベクトル ![]() ,
, ![]() は少し状況が異なる。
左固有ベクトル
は少し状況が異なる。
左固有ベクトル ![]() に対する議論は、右固有ベクトル
に対する議論は、右固有ベクトル ![]() と
ほぼ同じなので、ここでは
と
ほぼ同じなので、ここでは ![]() のみを考えることにする。
仮定より、当然
のみを考えることにする。
仮定より、当然 ![]() の各点
の各点 ![]() では
では ![]() を取ることはできるが、
を取ることはできるが、
![]() には定数倍の自由度があるので、
それを
には定数倍の自由度があるので、
それを ![]() 全体で滑らかになるように取れるかどうかは自明ではなく、
局所的な滑らかさが大域的な滑らかさの保証とはならない。
まずは局所的に滑らかなものが取れるかを考える。
全体で滑らかになるように取れるかどうかは自明ではなく、
局所的な滑らかさが大域的な滑らかさの保証とはならない。
まずは局所的に滑らかなものが取れるかを考える。
今、行列 ![]() を
を
今、![]() を、行列
を、行列 ![]() の
の ![]() 行目と
行目と ![]() 列目を除いた
列目を除いた ![]() 次小行列とすると、(C.4) より、
各
次小行列とすると、(C.4) より、
各 ![]() に対し
に対し
今、スカラー ![]() を
を ![]() 次元列ベクトル
次元列ベクトル ![]() の第
の第 ![]() 行成分、
行成分、
![]() を
を ![]() からその
からその ![]() 行目を除いた
行目を除いた ![]() 次元列ベクトル、
次元列ベクトル、
![]() を
を ![]() の第
の第 ![]() 列ベクトルを表すものとすると、
同次の線形方程式
列ベクトルを表すものとすると、
同次の線形方程式
(C.9) は、
(C.8) の ![]() 行目の方程式を除き、
行目の方程式を除き、
![]() 目の成分
目の成分 ![]() の部分を分けて書いたものになっているので、
(C.4) と (C.7) より、
(C.8) と (C.9) が同等であることがわかる。
の部分を分けて書いたものになっているので、
(C.4) と (C.7) より、
(C.8) と (C.9) が同等であることがわかる。
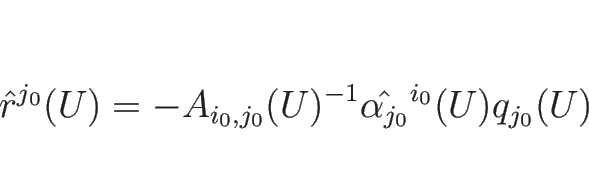
よって、(C.10) の複号を同順とした組は、
いずれも ![]() で
で ![]() と同程度の滑らかさを持つ
(C.5) の解となることがわかる。
これにより、局所的には滑らかな固有ベクトルが取れることが示された。
と同程度の滑らかさを持つ
(C.5) の解となることがわかる。
これにより、局所的には滑らかな固有ベクトルが取れることが示された。
ただし、次の例に見られるように、
(C.4) を満たす一般の行列 ![]() に対しては、
(C.5) の滑らかな解が大域的に取れるとは限らない。
に対しては、
(C.5) の滑らかな解が大域的に取れるとは限らない。
![]() を
を ![]() 平面から原点中心の円を、
あるいは原点 1 点を除いた領域とする。
平面から原点中心の円を、
あるいは原点 1 点を除いた領域とする。
![]() に対して、行列
に対して、行列 ![]() を極座標表示して、
を極座標表示して、
![\begin{displaymath}
A
=
\left[\begin{array}{cc}
1-\cos\theta & -\sin\theta\\
...
...\
y/\sqrt{x^2+y^2} & -1-x/\sqrt{x^2+y^2}
\end{array}\right]
\end{displaymath}](img1496.png)
このとき、(C.11) より
![]() の解は
の解は
![]() となるが、
(C.12) の
となるが、
(C.12) の ![]() は、
原点の回りの 1 周に関して半回転しかしない単位ベクトル場になっていて、
は、
原点の回りの 1 周に関して半回転しかしない単位ベクトル場になっていて、
![]() 、すなわち
、すなわち ![]() 軸の正の部分で不連続 (
軸の正の部分で不連続 (![]() 軸の両側で逆向きのベクトル)、
それ以外では滑らかな解となる。
一方、
軸の両側で逆向きのベクトル)、
それ以外では滑らかな解となる。
一方、
つまり、![]() が滑らかなので、確かに局所的には滑らな解 (
が滑らかなので、確かに局所的には滑らな解 (![]() か
か ![]() のどちらか) が必ず取れるが、
のどちらか) が必ず取れるが、
![]() 全体で滑らかな解を取ることはできない。
この例は、(C.10) で言えば、
その式の
全体で滑らかな解を取ることはできない。
この例は、(C.10) で言えば、
その式の ![]() の部分を、
の部分を、![]() 全体で一方の符号に統一できない
ようなものになっている。
全体で一方の符号に統一できない
ようなものになっている。
なおこの例は、![]() が単連結ではないし、
またこの
が単連結ではないし、
またこの ![]() は (C.3) の
形であるわけでもないので、
保存則方程式の固有ベクトルに対する反例、
すなわち
は (C.3) の
形であるわけでもないので、
保存則方程式の固有ベクトルに対する反例、
すなわち ![]() の固有ベクトルとして
の固有ベクトルとして ![]() 全体では滑らかなものが取れない、
という例を与えていることには必ずしもなっていない。
全体では滑らかなものが取れない、
という例を与えていることには必ずしもなっていない。
実際、(C.3) のように ![]() が
が ![]() に
近い形をしていると上の例のような回転行列のようなものは作りにくいので、
もしかすると保存則方程式の (C.3) の形の場合は、
このような例が構成できず、
よって
に
近い形をしていると上の例のような回転行列のようなものは作りにくいので、
もしかすると保存則方程式の (C.3) の形の場合は、
このような例が構成できず、
よって ![]() 全体で滑らかな
全体で滑らかな ![]() が
取れることが示されるのかもしれないが、
それは (C.3) の形であることを使用した
議論を必要とするはずであり、
少なくとも簡単にはどちらとも結論づけられない。
が
取れることが示されるのかもしれないが、
それは (C.3) の形であることを使用した
議論を必要とするはずであり、
少なくとも簡単にはどちらとも結論づけられない。
竹野茂治@新潟工科大学