今、![]() 上のスカラー値関数
上のスカラー値関数 ![]() が、
が、
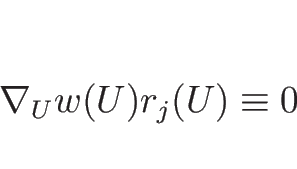
(3.6) の解 ![]() に対し、
に対し、
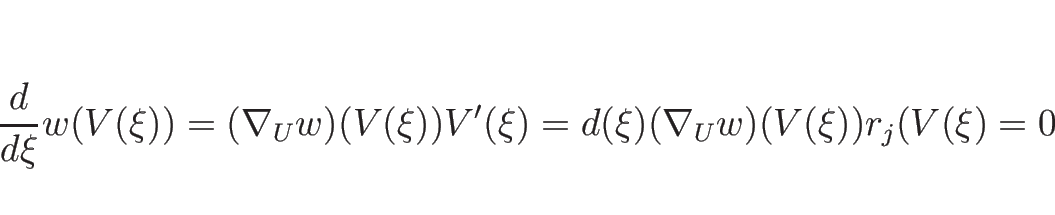
![]() が
が ![]() 内で滑らかで、かつ 0 ではないベクトルであるとき、
内で滑らかで、かつ 0 ではないベクトルであるとき、
![]() 内の各点
内の各点 ![]() に対し、その
に対し、その ![]() のある
近傍
のある
近傍 ![]() (
(
![]() 上で次が成り立つ。
上で次が成り立つ。
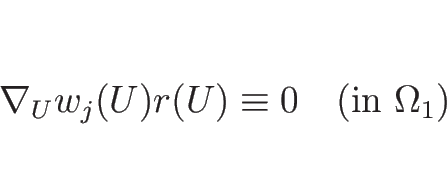
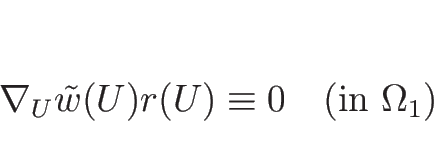
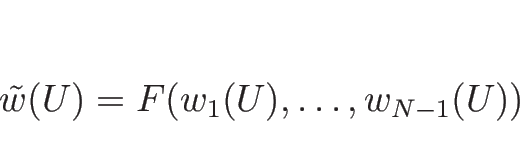
この命題の証明は、C.2 節で行う。
なお、この命題では ![]() 全体ではなく、局所的、
すなわち各点
全体ではなく、局所的、
すなわち各点 ![]() の近傍
の近傍 ![]() 上での
リーマン不変量の存在しか示していないが、
個別の保存則方程式の例では考えている領域
上での
リーマン不変量の存在しか示していないが、
個別の保存則方程式の例では考えている領域 ![]() 全体で
統一したリーマン不変量を取ることができることも多いし、
また一般の場合でも、必要なら
全体で
統一したリーマン不変量を取ることができることも多いし、
また一般の場合でも、必要なら ![]() を小さく取ることにより、
を小さく取ることにより、
![]() 全体でのリーマン不変量が存在するようにすることも可能である。
よって以後は、
全体でのリーマン不変量が存在するようにすることも可能である。
よって以後は、![]() 全体で滑らかなリーマン不変量が存在する
と仮定して話を進める。
全体で滑らかなリーマン不変量が存在する
と仮定して話を進める。
ベクトル場 ![]() の積分曲線上
の積分曲線上 ![]() -リーマン不変量は定数であるが、
逆に
-リーマン不変量は定数であるが、
逆に ![]() -リーマン不変量を定数にするものとして
-リーマン不変量を定数にするものとして ![]() の積分曲線が
得られることを示そう。
の積分曲線が
得られることを示そう。
![]() 個の
個の ![]() -リーマン不変量
-リーマン不変量 ![]() , ...,
, ..., ![]() は、
は、
![]() , ...,
, ...,
![]() が線形独立であるから、
が線形独立であるから、
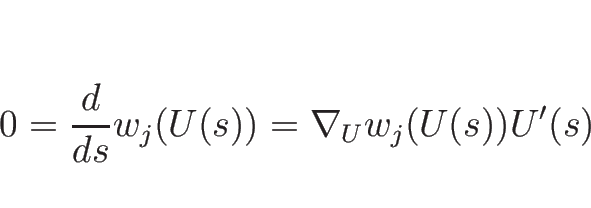
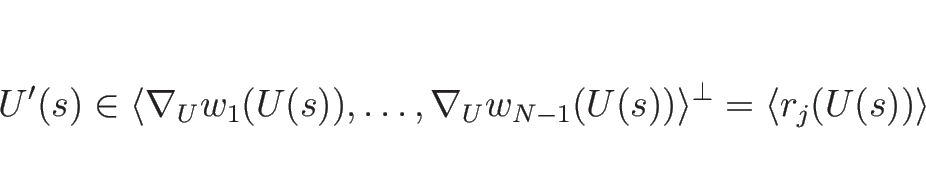
しかも、命題 3.1 の 1. より
(詳しくは C.2 節で示す通り)、
![]() となる関数
となる関数 ![]() を追加すれば、
を追加すれば、
![]() ,...,
,...,
![]() が線形独立となり、
よって
が線形独立となり、
よって ![]() と
と
![]() が 1 対 1 となるので、
不変集合 (3.11) は確かに 1 本の曲線であることがわかる。
が 1 対 1 となるので、
不変集合 (3.11) は確かに 1 本の曲線であることがわかる。
なお、![]() -膨張波曲線
-膨張波曲線 ![]() は、
微分方程式 (3.10) の解のうち、
は、
微分方程式 (3.10) の解のうち、
![]() が増加する方向であるが、真性非線形性の仮定により
が増加する方向であるが、真性非線形性の仮定により
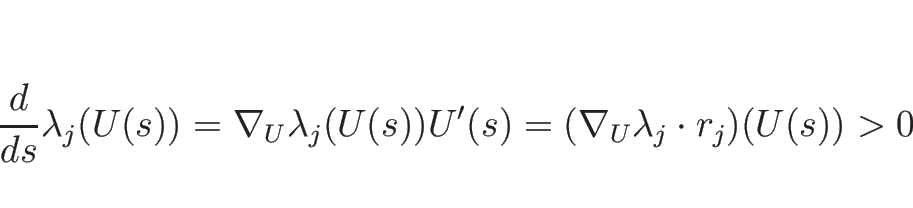
竹野茂治@新潟工科大学