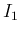
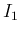 の値であるが、
の値であるが、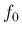 ,
, 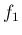 ともに留数を利用しても
積分値は求まらず、別な方法が必要になる。
ともに留数を利用しても
積分値は求まらず、別な方法が必要になる。
数学辞典[1]を見ると、付録 (公式 9 V) に
が書かれている。また、数表[2] (2.6.5 p491) には、 の値が記されていて、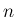 が奇数の場合はこれが Bernoulli 数で表されている。
が奇数の場合はこれが Bernoulli 数で表されている。
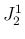 が
が 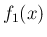 の積分になっていて
の積分になっていて 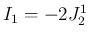 なので、
なので、
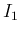 より一般の
より一般の 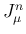 が分かれば
が分かれば 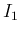 の値もわかることになる。
本節ではこの
の値もわかることになる。
本節ではこの 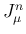 の値を考える。
の値を考える。
この値を求めるために、非負の関数に対する無限和と積分の 順序交換の定理を用いる。
実数上の任意の区間 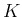 と、
と、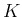 上の非負の関数列
上の非負の関数列 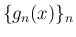 に
対し、
に
対し、
この定理は、Lebesgue 単調収束定理から直ちに従う。
さて 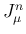 の値を計算する。まず、
の値を計算する。まず、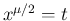 と置換すると、
と置換すると、
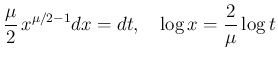
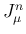 は
と書ける。ここで、
は
と書ける。ここで、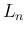 は
は
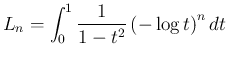
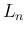 には
には 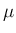 は含まれず、そして
は含まれず、そして 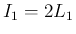 となる。
となる。
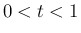 では、
では、
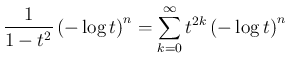
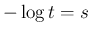 とすると、
とすると、
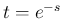 ,
,
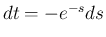 より、
より、
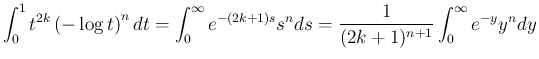
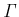 関数で書け、
関数で書け、
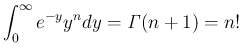
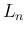 は
は
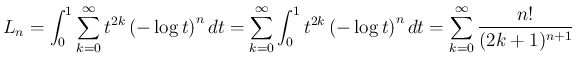
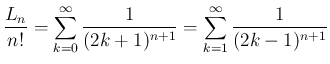
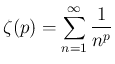
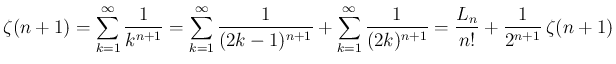
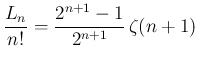
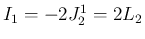 に関しては、
良く知られているように
に関しては、
良く知られているように
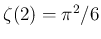 なので、よって
なので、よって 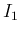 は
は
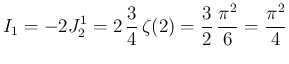
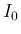 は
は
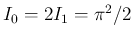 となる。
となる。
竹野茂治@新潟工科大学