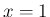
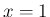 での反転
での反転 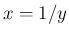 によって、
によって、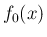 は
となるので、この置換により積分
は
となるので、この置換により積分
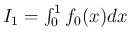 は、
は、
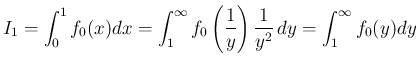
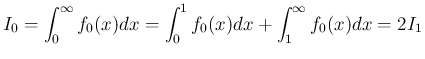
 乗の積分値
乗の積分値 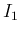 のみを考えればよいことになる。
のみを考えればよいことになる。
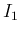 の値も容易には求まらないが、部分積分すると、
の値も容易には求まらないが、部分積分すると、
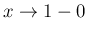 では、
では、
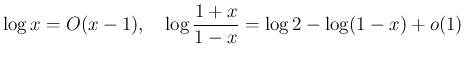
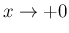 では、
では、
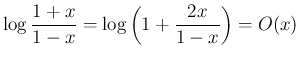
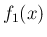 を
とすると、
(4),(5) より
となる。
この
を
とすると、
(4),(5) より
となる。
この 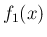 は、偶関数で、
は、偶関数で、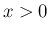 では正であり、
では正であり、
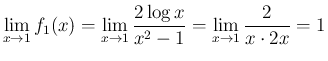
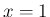 では
では 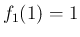 とすれば連続となり、
とすれば連続となり、
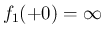 、
、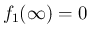 となるが、
となるが、
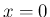 付近、
付近、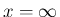 付近でも可積分となることは容易にわかる。
付近でも可積分となることは容易にわかる。
さらに、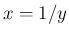 の反転で、
の反転で、
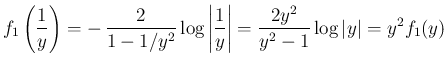
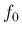 の (3) と同じ性質を持つので、
の (3) と同じ性質を持つので、
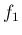 に対しても
に対しても
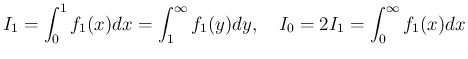
さらにもう一つ別な置換も紹介する。
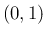 での
での 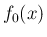 の積分で
の積分で 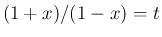 と置換すると
と置換すると 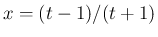 ,
,
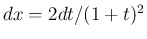 となり、
となり、
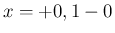 は
は 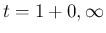 に対応し、
に対応し、
竹野茂治@新潟工科大学