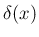
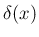 は通常の関数ではなく超関数で、
通常は
のようにみなされ、連続関数
は通常の関数ではなく超関数で、
通常は
のようにみなされ、連続関数 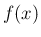 に対し
のような性質を持つものとして知られている。
当然、通常の実数値関数にはそういうものはなく、
数学では
に対し
のような性質を持つものとして知られている。
当然、通常の実数値関数にはそういうものはなく、
数学では
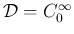 上の汎関数 (
上の汎関数 (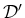 ) として、
を満たすものとして定義される。
) として、
を満たすものとして定義される。
一般に超関数
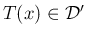 に
に 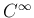 関数
関数 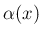 をかけた
をかけた 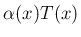 も
も 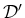 上に定義でき、それは
上に定義でき、それは
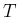 の微分
の微分 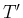 は、
の部分積分形で定義される。
は、
の部分積分形で定義される。
さて気になった式というのは、デルタ関数 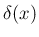 に
に 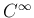 関数
関数 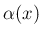 をかけた
をかけた
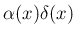 の導関数であるが、
当然積の微分から、
の導関数であるが、
当然積の微分から、
竹野茂治@新潟工科大学