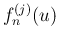
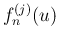 (
(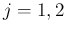 ) を上からおさえる
可積分関数
) を上からおさえる
可積分関数 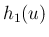 の存在を、実際にそれを構成することで示す。
なお、
の存在を、実際にそれを構成することで示す。
なお、
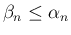 より
より
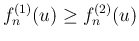 なので、
本節では主に
なので、
本節では主に 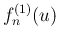 のみを考える。
のみを考える。
まず、
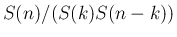 については、
(35) を満たす
については、
(35) を満たす 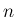 と
と
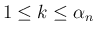 に
対しては
に
対しては 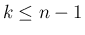 なので、(23) より
なので、(23) より
次は 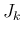 であるが、
であるが、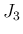 は各点収束では単純であるが、
上からおさえるのは案外難しい。
は各点収束では単純であるが、
上からおさえるのは案外難しい。
まずは、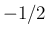 倍がついていることで対数部分を上からおさえることが
できなくなっているため、
倍がついていることで対数部分を上からおさえることが
できなくなっているため、
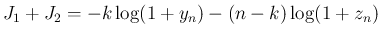 の
定数倍を利用する。
の
定数倍を利用する。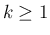 であり、また (35) を
満たす
であり、また (35) を
満たす 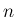 については
については 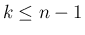 なので、
なので、
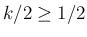 ,
,
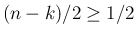 であるから、
であるから、
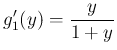
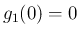 より
より 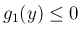 、すなわち
、すなわち
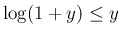 が
得られるので、(29) より、
が
得られるので、(29) より、
また、
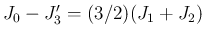 については、
(30) の変形を用いるが、ここで
については、
(30) の変形を用いるが、ここで 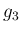 に対して、
に対して、
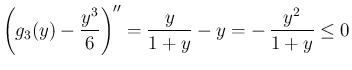
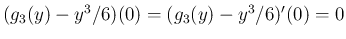 より (40) が成り立つことがわかる。
これを用いると、
より (40) が成り立つことがわかる。
これを用いると、
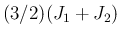 は、(29) より
は、(29) より
(42) の右辺の真ん中の項の 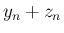 は、
係数が 0 以上なので上から評価すればよいが、
3 番目の項は係数が負なので、下から評価しなければならず、
それで難易度がだいぶ変わってしまう。
まずは、
は、
係数が 0 以上なので上から評価すればよいが、
3 番目の項は係数が負なので、下から評価しなければならず、
それで難易度がだいぶ変わってしまう。
まずは、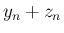 の上からの評価から。
の上からの評価から。
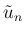 は、
は、
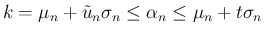 より
より
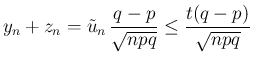
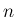 に対しては、
となり、よって
に対しては、
となり、よって
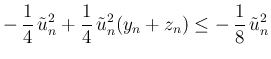
次は 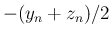 の上からの評価。
この場合、(43) に対応するような、
の上からの評価。
この場合、(43) に対応するような、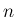 に
よらない
に
よらない 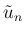 の下限は存在しないが、
の下限は存在しないが、
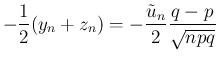
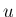 の 1 次式なので、そのように評価する。
(20) に従い、次のように
の 1 次式なので、そのように評価する。
(20) に従い、次のように 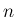 によらない場合分けを
行って考える。
によらない場合分けを
行って考える。
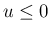 の場合
の場合
この場合は (20) より
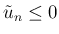 で、
で、
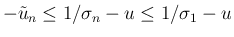 なので (
なので (
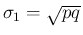 )、
)、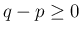 より、
より、
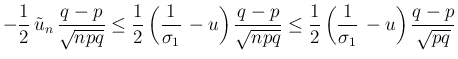
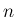 によらない
によらない 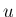 の一次式でおさえられる。
の一次式でおさえられる。
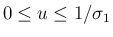 の場合
の場合
この場合は、(20) より
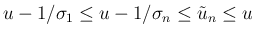 なので、
なので、
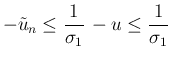
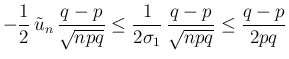
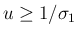 の場合
の場合
この場合は、
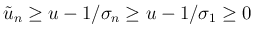 なので、
なので、
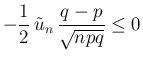
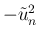 も、ほぼ
も、ほぼ 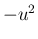 であるが、
上と同じ場合分けで考える。
であるが、
上と同じ場合分けで考える。
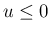 の場合
の場合
この場合は
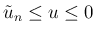 なので、
なので、
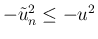 となる。
となる。
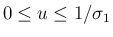 の場合
の場合
この場合は
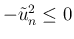 と評価する。
と評価する。
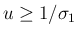 の場合
の場合
この場合は、
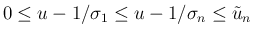 なので、
なので、
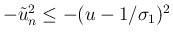 と評価される。
と評価される。
以上をまとめると、(35), (44) を
満たす 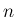 に対して、
に対して、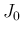 は、以下のようなもので評価されることになる。
は、以下のようなもので評価されることになる。
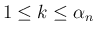 を仮定しているが、
を仮定しているが、
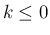 ,
,
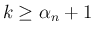 の
の 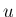 に対しては、
に対しては、
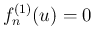 となり、
その場合は
となり、
その場合は
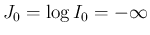 と見ることができるから、
上の評価は、すべての
と見ることができるから、
上の評価は、すべての 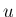 に対して成り立つことになる。
これらは
に対して成り立つことになる。
これらは 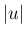 が大きいところでは
が大きいところでは 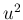 の係数が
の係数が 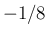 の 2 次式なので、
の 2 次式なので、
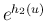 は
は 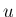 に関して可積分となり、これで
に関して可積分となり、これで 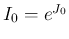 が上から
おさえられることになる。
とおさえられることになり、この右辺は
が上から
おさえられることになる。
とおさえられることになり、この右辺は 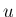 に関して
に関して
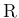 上可積分なので、
これでルベーグ収束定理の
上可積分なので、
これでルベーグ収束定理の 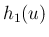 に相当するものが取れたことになる。
に相当するものが取れたことになる。
よって、ルベーグ収束定理と (12), (18), (36) により、
![\begin{eqnarray*}\lim_{n\rightarrow \infty}{\mathrm{Prob}\left\{\frac{x-\mu_n}{\...
...}}f_0(u)\chi_{(-\infty,t]}(u)du
\\ &=&
\int_{-\infty}^tf_0(u)du\end{eqnarray*}](img244.png)
竹野茂治@新潟工科大学