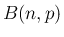 (
(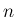 は自然数、
は自然数、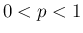 ) に従う
確率変数
) に従う
確率変数 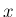 に対し、
その平均
に対し、
その平均 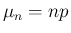 、標準偏差
、標準偏差
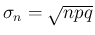 (
(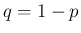 ) に
対して
) に
対して
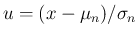 と
と 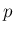 を固定したときに、
その
を固定したときに、
その
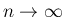 のときの確率関数
のときの確率関数 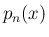 と
と 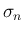 の積の
極限が、標準正規分布の密度関数
の積の
極限が、標準正規分布の密度関数 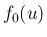 に収束すること、すなわち
に収束すること、すなわち
[1] では、二項分布 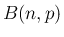 (
(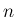 は自然数、
は自然数、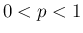 ) に従う
確率変数
) に従う
確率変数 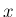 に対し、
その平均
に対し、
その平均 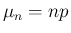 、標準偏差
、標準偏差
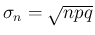 (
(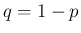 ) に
対して
) に
対して
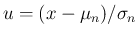 と
と 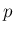 を固定したときに、
その
を固定したときに、
その
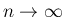 のときの確率関数
のときの確率関数 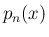 と
と 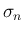 の積の
極限が、標準正規分布の密度関数
の積の
極限が、標準正規分布の密度関数 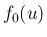 に収束すること、すなわち
に収束すること、すなわち
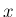 は本来
は本来 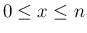 の整数の値のみを取る変数であるが、
と
の整数の値のみを取る変数であるが、
と 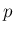 を固定した場合には一般には
を固定した場合には一般には 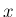 は整数にはならず、
厳密にはその議論に修正が必要である。それは 5 節で行う。
は整数にはならず、
厳密にはその議論に修正が必要である。それは 5 節で行う。
また、(1) は各点収束の意味での
ド・モアブル=ラプラスの中心極限定理であるが、
分布関数の意味での中心極限定理は、任意の実数 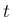 に対して、
に対して、
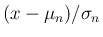 ) の分布関数の
極限が、
標準正規分布の分布関数に収束することを意味している。
) の分布関数の
極限が、
標準正規分布の分布関数に収束することを意味している。
この式は、形式的にはほぼ各点収束の極限の式 (1) を、
![$(-\infty,t]$](img21.png) の範囲で両辺積分した形になっているのであるが、
その積分は無限幅での広義積分なので、
その積分と
の範囲で両辺積分した形になっているのであるが、
その積分は無限幅での広義積分なので、
その積分と 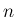 に関する極限との順序交換ができるという保証を与えなければ
その厳密な証明にはならない。
に関する極限との順序交換ができるという保証を与えなければ
その厳密な証明にはならない。![$[s,t]$](img22.png) のような有限な範囲での積分した形、
すなわち
のような有限な範囲での積分した形、
すなわち
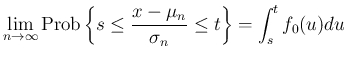
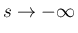 とするのも同じで、
やはり
とするのも同じで、
やはり 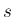 の極限と
の極限と 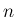 の極限の順序交換可能の保証が必要となる。
の極限の順序交換可能の保証が必要となる。
例えば、
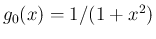 は
は
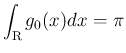
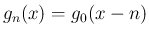 に対し
となるが、これは積分と
に対し
となるが、これは積分と 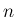 の極限を入れ替えた式
には一致しない。
の極限を入れ替えた式
には一致しない。
積分範囲が有限であれば、関数が一様収束すれば積分の極限と 極限の積分は一致するが、積分範囲が無限である広義積分では それでは不十分である。
本稿では、それを保証するために以下のルベーグ収束定理を用いる。
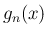 が各
が各 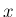 に対して
に対して
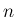 に無関係な
に無関係な 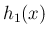 があって、
となるとき、
があって、
となるとき、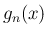 も
も 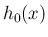 も
も
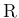 上可積分で、
上可積分で、
本来ルベーグ収束定理は、
正でない値を取る関数にも適用できるのであるが、
本稿では正の関数だけ考えれば十分であるので、この形で紹介しておく。
また、上の
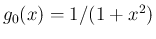 の例の場合は、
(6) は満たしているが、
(7) を満たすような
の例の場合は、
(6) は満たしているが、
(7) を満たすような 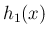 を
取ることができないため、(8) が
成り立たない。
を
取ることができないため、(8) が
成り立たない。
よって、分布関数の収束性を示すためには、
(7) を満たすような 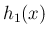 の
存在を示すことが必要となる。
それは 6 節で考える。
の
存在を示すことが必要となる。
それは 6 節で考える。
竹野茂治@新潟工科大学