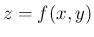
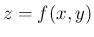 が
が 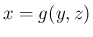 と解けたと仮定するが、
解けることは、例えば
と解けたと仮定するが、
解けることは、例えば
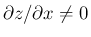 を満たしていれば可能である (厳密には陰関数定理)。
を満たしていれば可能である (厳密には陰関数定理)。
そしてこの場合、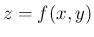 と
と 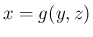 は同じ式を意味することになるので、
一方に他方を代入した、
は同じ式を意味することになるので、
一方に他方を代入した、
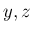 の恒等式で、
は
の恒等式で、
は 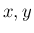 の恒等式になることに注意する。
の恒等式になることに注意する。
これは、少し具体例で説明する。「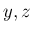 の恒等式」とは、
すべての
の恒等式」とは、
すべての 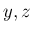 について成り立つ式、という意味で、
「方程式」とは異なる。
例えば、
について成り立つ式、という意味で、
「方程式」とは異なる。
例えば、
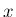 について解いたものが
について解いたものが 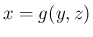 なので、
なので、
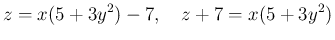
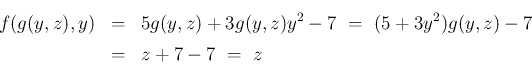
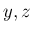 に対して (6) となるし、
逆に (8) を (9) に代入すれば、
に対して (6) となるし、
逆に (8) を (9) に代入すれば、
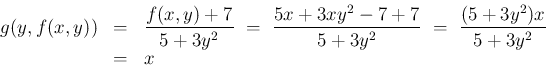
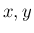 に対して (7) となることが
わかる。
に対して (7) となることが
わかる。
竹野茂治@新潟工科大学