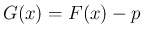 とおけば、これは
とおけば、これは 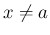 の
の 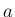 の近くで定義され、
の近くで定義され、
一般に極限 (8) は、
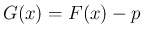 とおけば、これは
とおけば、これは 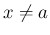 の
の 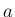 の近くで定義され、
の近くで定義され、
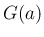 を
を 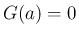 と定義すれば、
と定義すれば、
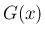 は
は 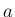 の近くで定義され、
(8) は
の近くで定義され、
(8) は 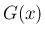 が
が 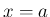 で連続、ということと同値になる。
で連続、ということと同値になる。
これと同様にして、(1) から 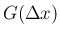 を
を
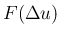 を
と定義すると、
を
と定義すると、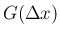 ,
, 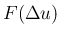 はそれぞれ 0 で連続となり、
それがそれぞれ (1), (2) の仮定と同値になる。
はそれぞれ 0 で連続となり、
それがそれぞれ (1), (2) の仮定と同値になる。
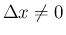 のときは、(11) より
のときは、(11) より
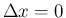 のときも両辺 0 となるので成立する。
同様に、
のときも両辺 0 となるので成立する。
同様に、
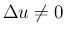 のときは、(12) より
となるが、これも
のときは、(12) より
となるが、これも 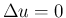 のときも両辺 0 となり成立する。
のときも両辺 0 となり成立する。
これらにより、
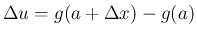 とし、
とし、
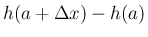 を
を 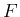 ,
, 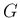 ,
, 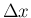 で表すと (
で表すと (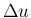 が 0 であるかないかに関わらず)、
が 0 であるかないかに関わらず)、
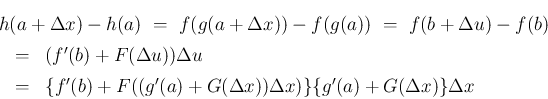
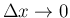 とすると、
とすると、
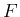 ,
, 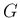 の 0 での連続性、およびその値 (極限) が 0 であることから、
右辺は
の 0 での連続性、およびその値 (極限) が 0 であることから、
右辺は 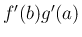 に収束することがわかる。
よって、
に収束することがわかる。
よって、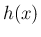 は
は 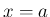 で微分可能で、その微分係数は
で微分可能で、その微分係数は 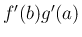 となる。
これで公式 2.6 が証明されたことになる。
となる。
これで公式 2.6 が証明されたことになる。
この証明の場合は、微分可能性を 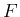 ,
, 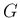 を使って表現することにより
を使って表現することにより
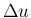 での割算を避けていて、
それにより前節の証明のような場合分けが必要なくなっている。
しかしこの証明の場合メリットはそれ位で、
逆にこの証明だと元々の合成関数の微分が
どうしてその形になるのかが見えにくくなっていて、
よってそれほどいい証明とも言えないと思う。
での割算を避けていて、
それにより前節の証明のような場合分けが必要なくなっている。
しかしこの証明の場合メリットはそれ位で、
逆にこの証明だと元々の合成関数の微分が
どうしてその形になるのかが見えにくくなっていて、
よってそれほどいい証明とも言えないと思う。
竹野茂治@新潟工科大学