2 4 次の行列式
この節では、[1] で説明している 4 次の行列式の計算方法を紹介する。
![\begin{displaymath}
A = [a_{i,j}]
= \left[\begin{array}{cccc}%
a_{1,1}&a_{1,2}&...
...&a_{3,4}\\
a_{4,1}&a_{4,2}&a_{4,3}&a_{4,4}\end{array}\right]
\end{displaymath}](img1.gif)
とする。
なお、本稿ではこのように行列の成分の 2 重の添え字を `,' で区切って書くことにする。
- まず、3 次の行列式に対するサラス-関の方法と同じように、
斜めに 4 つずつかけてできる 8 項を作る。
ただし、3 次の場合とは違い、対角成分の積
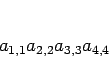
には 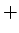 を、その一つ下の斜めの積
を、その一つ下の斜めの積
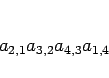
には 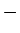 を、という具合にこちらの方向の積の 4 項には
入れ違いに
を、という具合にこちらの方向の積の 4 項には
入れ違いに 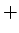 ,
, 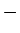 をつける。
右上から左下の方向の斜めの積も、対角線の積
をつける。
右上から左下の方向の斜めの積も、対角線の積
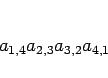
には 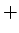 、その下には順に
、その下には順に 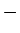 ,
, 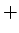 ,
, 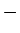 を付ける。
それらを加えたものをまず
を付ける。
それらを加えたものをまず 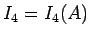 とする:
とする:
-
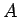 の 2 行目を 4 行目に降ろし、3, 4 行目をひとつずつ上げて
2, 3 行目にした行列
の 2 行目を 4 行目に降ろし、3, 4 行目をひとつずつ上げて
2, 3 行目にした行列 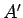 を考える:
を考える:
![\begin{displaymath}
A'
= \left[\begin{array}{cccc}%
a_{1,1}&a_{1,2}&a_{1,3}&...
...a_{4,4}\\
a_{2,1}&a_{2,2}&a_{2,3}&a_{2,4}\end{array}\right]
\end{displaymath}](img16.gif)
これに対して 1. と同じ計算を行う (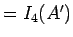 )。
)。
-
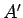 に対し、2 と同じ操作を行った行列
に対し、2 と同じ操作を行った行列 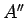 に対し、
1. と同じ計算を行う (
に対し、
1. と同じ計算を行う (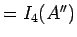 ):
):
![\begin{displaymath}
A''
= \left[\begin{array}{cccc}%
a_{1,1}&a_{1,2}&a_{1,3}...
...a_{2,4}\\
a_{3,1}&a_{3,2}&a_{3,3}&a_{3,4}\end{array}\right]
\end{displaymath}](img20.gif)
- 結果として、これら 3 つの和が
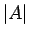 となる:
となる:
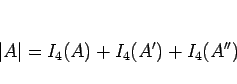 |
(2) |
という方法である。
サラス-関と同様の計算である 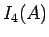 だけでは 8 項しか項が得られないが、
4 次の行列式には
だけでは 8 項しか項が得られないが、
4 次の行列式には 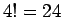 項が必要で、
同じ行、同じ列に入らない 4 つの要素のすべての組を作るために
このような行の入れかえを行っている。
項が必要で、
同じ行、同じ列に入らない 4 つの要素のすべての組を作るために
このような行の入れかえを行っている。
ただし、3 次の場合とは符号のつけ方も大きく違っていて、
3 次の場合は、左上から右下への積は全部 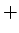 、
右上から左下への積は全部
、
右上から左下への積は全部 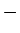 であるが、
4 次の場合は、左上から右下への積には
であるが、
4 次の場合は、左上から右下への積には 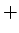 と
と 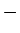 が交互に現れ、
右上から左下への積も同じ形で符号をつける形になっている。
が交互に現れ、
右上から左下への積も同じ形で符号をつける形になっている。
この符号に関する話は後で考察するとして、
まず先に行の入れ替えですべての項を重なりなく作る方法について
考えることにする。
竹野茂治@新潟工科大学
2008年7月26日
![\begin{displaymath}
A = [a_{i,j}]
= \left[\begin{array}{cccc}%
a_{1,1}&a_{1,2}&...
...&a_{3,4}\\
a_{4,1}&a_{4,2}&a_{4,3}&a_{4,4}\end{array}\right]
\end{displaymath}](img1.gif)
![]() だけでは 8 項しか項が得られないが、
4 次の行列式には
だけでは 8 項しか項が得られないが、
4 次の行列式には ![]() 項が必要で、
同じ行、同じ列に入らない 4 つの要素のすべての組を作るために
このような行の入れかえを行っている。
項が必要で、
同じ行、同じ列に入らない 4 つの要素のすべての組を作るために
このような行の入れかえを行っている。
![]() 、
右上から左下への積は全部
、
右上から左下への積は全部 ![]() であるが、
4 次の場合は、左上から右下への積には
であるが、
4 次の場合は、左上から右下への積には ![]() と
と ![]() が交互に現れ、
右上から左下への積も同じ形で符号をつける形になっている。
が交互に現れ、
右上から左下への積も同じ形で符号をつける形になっている。