の形の式のことを言う。
(20)
を満たす
(20)
(20) の場合、![]() となる
となる ![]() が少なくとも一つはあるので、
それを使って
が少なくとも一つはあるので、
それを使って
逆に、
![]() が残りの他のものの一次結合であれば、
が残りの他のものの一次結合であれば、
「そのいずれかひとつが、他の残りのものの一次結合となる」と言いかえることもできる。
例えば、平行でない 2 つの平面ベクトルや、 一つの平面に乗らない 3 つの空間ベクトルなどは一次独立であるが、 平行な 2 つのベクトルや、一つの平面上の 3 つ以上のベクトルなどは 一次従属である。
![]() 次正方行列
次正方行列
この証明は、1. と 3. が 同値であることが言えれば、2. は、
1.となって 1. と 2. が 同値であることも言えるから、 1. と 3. の同値性のみ 証明すればよい。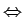
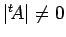
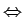
が一次独立
2.
今度は 3. ![]() 1.
を考えるが、この証明に帰納法を用いる。
1.
を考えるが、この証明に帰納法を用いる。
![]() のときは明らかに成り立つから、
のときは明らかに成り立つから、
![]() 次では 1., 2.,
3. の同値性が言えているとする。
次では 1., 2.,
3. の同値性が言えているとする。
3. ![]() 1. を示すために、
3. であって、かつ 1. でないとして
矛盾を導くことにする。
つまり、
1. を示すために、
3. であって、かつ 1. でないとして
矛盾を導くことにする。
つまり、
と仮定する。は一次独立で、 かつ
である
任意の ![]() (
(![]() ) に対し、
) に対し、![]() を
を ![]() 列目で展開すると、
列目で展開すると、
(21)
(22)
よって、すべての ![]() に対して
に対して
![]() となることになるが、
となることになるが、
![]() も任意であったので、結局この場合すべての
も任意であったので、結局この場合すべての ![]() に対して
に対して
![]() であることになる。
であることになる。
今、![]() から
から ![]() 行目と
行目と ![]() 列目を取り除いた行列を
列目を取り除いた行列を
![]() と書くことにする (よって
と書くことにする (よって
![]() )。
すると、
)。
すると、
![]() は
は ![]() 次の正方行列で、
次の正方行列で、
![]() なので、
帰納法の仮定により、その
なので、
帰納法の仮定により、その ![]() 個の行ベクトルは一次従属となる。
個の行ベクトルは一次従属となる。
よって、任意の ![]() に対し、
に対し、
(23)
(24)
今、もし ![]() であると、
であると、
![]() でかつ
でかつ
この (24) をすべての ![]() で考えれば、
結局
で考えれば、
結局 ![]() に対し
に対し
さて、この式の右辺は対角行列で、 その行列式は 1 列目から展開していけばわかるが、
よって、3. であって、かつ 1. でない
とすると矛盾が起こることになり、ゆえに
3. ![]() 1. が言えることになる。
1. が言えることになる。
![]() に対して、
に対して、![]() 行列
行列
(25)
今、
次に、2. ![]() 1.
を、
1.
を、![]() に関する帰納法で証明する。
に関する帰納法で証明する。
![]() のときは、定理 9 より明らかに成り立つので、
のときは、定理 9 より明らかに成り立つので、
![]() として、
として、![]() のときに成り立つとして
のときに成り立つとして ![]() のときに
成り立つことを示す。そして、そのために、
2. であって、かつ 1. でない
として矛盾を導く。すなわち、
のときに
成り立つことを示す。そして、そのために、
2. であって、かつ 1. でない
として矛盾を導く。すなわち、
と仮定する。は一次独立で、かつ、 すべての
に対して、
である
今、![]() から
から ![]() 列目を取り除いた
列目を取り除いた ![]() 行列
行列
![]() を
を ![]() と書くこととし、
その行ベクトルを上から順に
と書くこととし、
その行ベクトルを上から順に
![]() と書くことにする。
と書くことにする。
この ![]() に対しても、仮定よりすべての
に対しても、仮定よりすべての
![]() に対して、
に対して、
(26)
(27)
この定理を用いれば、行列の階数 (ランク) と一次独立性の定理も証明できるので、
それもついでに紹介しておく。
![]() を
を ![]() 行列とし、
行列とし、![]() かつ
かつ ![]() のとき、
のとき、
![]() ,
,
![]() に対し
に対し
![]() 次の小行列式がすべて 0 なら、
次の小行列式がすべて 0 なら、![]() に対し、
に対し、
![]() 次の小行列式もすべて 0 となることが展開定理から容易に分かるので、
よって、
次の小行列式もすべて 0 となることが展開定理から容易に分かるので、
よって、![]() に対して
に対して
「を満たすような次以上の小行列式はすべて 0 で、
次 (および
以下の次数) の小行列式には、 少なくとも一つ 0 でないものがある」
これは、定理 10 より容易に示される。
![]() より、
より、
逆に、
![]() が一次独立なら、
行列
が一次独立なら、
行列
![]() を考えれば定理 10 より、
を考えれば定理 10 より、
![]() に関しても同様なので、ゆえに、
一次独立なベクトルの組の最大数と、
に関しても同様なので、ゆえに、
一次独立なベクトルの組の最大数と、
![]() は等しいことになる。
は等しいことになる。
竹野茂治@新潟工科大学