3 指数法則
次は、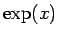 に対する指数法則などの基本性質を見ていく。
に対する指数法則などの基本性質を見ていく。
まず、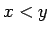 のとき、
のとき、
であるから、
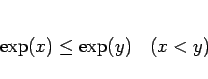 |
(18) |
の単調増加性が得られる。なお、実際にはこの等号も外すことができるが、
それは後で示す。
また、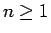 ,
, 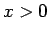 に対して、
に対して、
であるから、
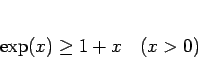 |
(19) |
が成り立ち、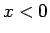 ならば (16), (19) より
ならば (16), (19) より
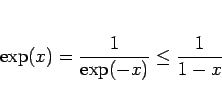 |
(20) |
が成り立つことがわかる。
(16), (19) より 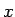 が正でも負でも
が正でも負でも 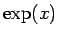 は常に正となるので、
(19), (20) から、漸近性質
は常に正となるので、
(19), (20) から、漸近性質
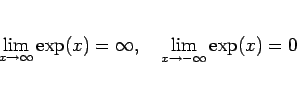 |
(21) |
が得られる (厳密にははさみうちの原理による)。
次は指数法則を考える。まず、自然数 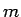 に対して、
に対して、
より、
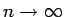 の極限を取れば
の極限を取れば
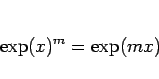 |
(22) |
が成り立つことがわかる。
また、(16) と組み合わせると
も成り立つので、以上を合わせると、整数 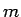 に対して、
に対して、
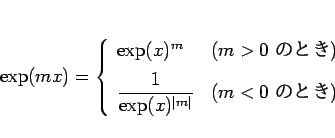 |
(23) |
が得られる。さらに、自然数 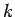 に対して、(22) より
に対して、(22) より
となるから、よって
となる。これと (23) を組み合わせれば、
整数 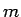 ,
, 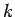 (
(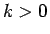 ) に対して、
) に対して、
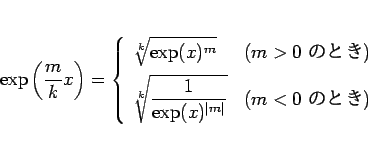 |
(24) |
となることもわかる。
これは、有理数 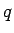 に対して「
に対して「
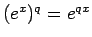 」を示したことに相当する。
しかし、実数
」を示したことに相当する。
しかし、実数 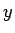 に対する「
に対する「
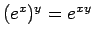 」を示すには、
一般の
」を示すには、
一般の 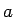 に対する「
に対する「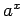 」が必要になるので、それはまだ示すことはできない。
」が必要になるので、それはまだ示すことはできない。
次は、
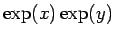 を考える。
を考える。
となるが、命題 4 により最後の式は 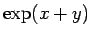 と 1 の積に収束するので、
と 1 の積に収束するので、
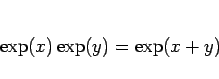 |
(25) |
が成り立つことになる。これは「
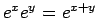 」に相当する。
」に相当する。
なお、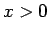 であれば (19) より
であれば (19) より 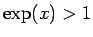 なので、
(25) より
なので、
(25) より 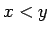 に対して
に対して
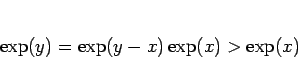 |
(26) |
が成り立つことがわかる。
これは、(18) の等号を外すことができることを
示したことになる。
(25) で 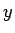 を
を 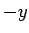 とすれば、(16) より
とすれば、(16) より
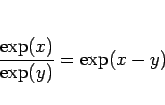 |
(27) |
が成り立つこともわかる。これは「
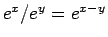 」に相当する。
」に相当する。
竹野茂治@新潟工科大学
2017年2月2日
![]() のとき、
のとき、
![]() ,
, ![]() に対して、
に対して、
![]() に対して、
に対して、
![]() を考える。
を考える。
![]() であれば (19) より
であれば (19) より ![]() なので、
(25) より
なので、
(25) より ![]() に対して
に対して