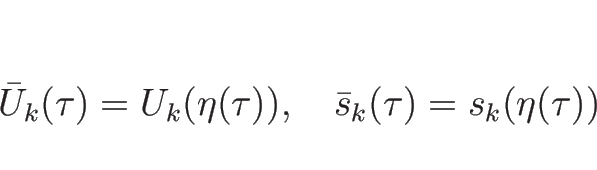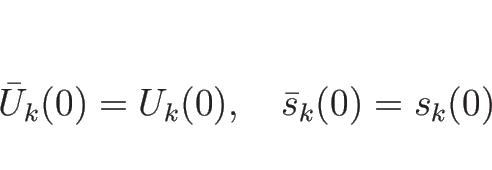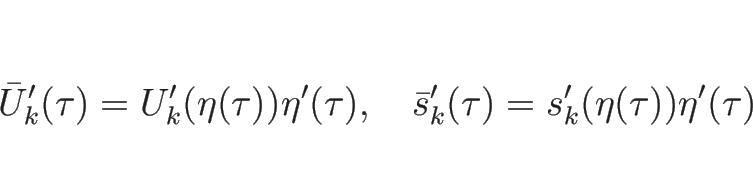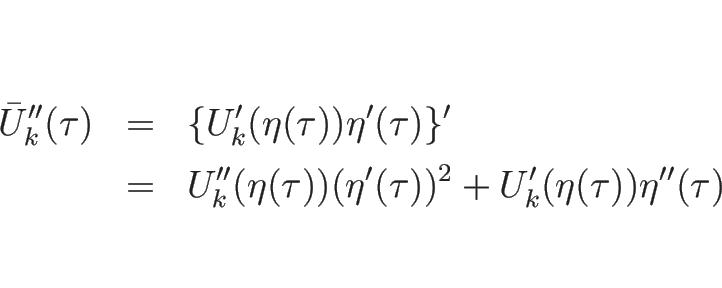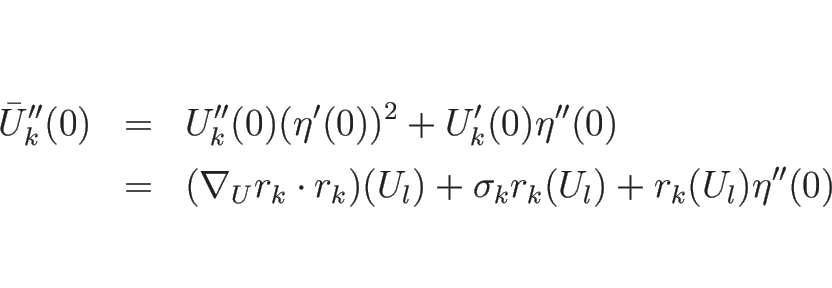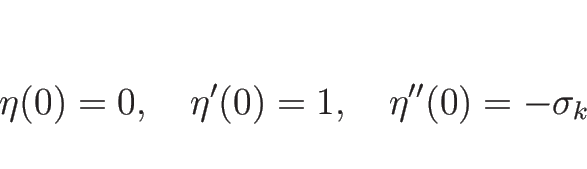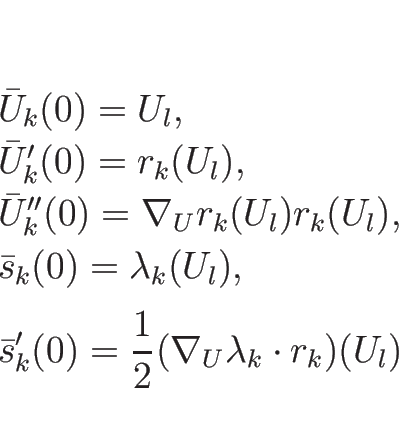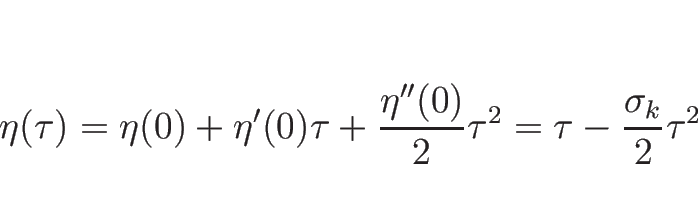4.5 ランキン-ユゴニオ条件を満たすベクトルの構造
4.2, 4.3 節で見たように、
不連続線と左右の解の値はランキン-ユゴニオ条件を
満たす必要があることがわかる。
よって、(4.1) の一番単純な不連続解は、
ランキン-ユゴニオ条件
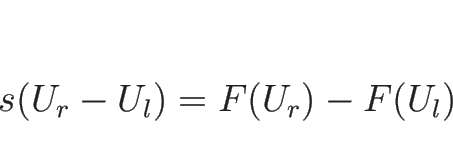 |
(4.74) |
を満たす定数ベクトル 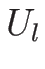 ,
, 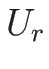 , と定数値
, と定数値 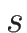 に対して、
に対して、
であることになる。
なお、この解は 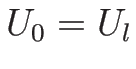 ,
, 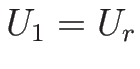 のときの初期条件
(3.9) を満たす解になっていて、
よってそのような初期値に対するリーマン問題の解になっている。
のときの初期条件
(3.9) を満たす解になっていて、
よってそのような初期値に対するリーマン問題の解になっている。
条件式 (4.25) は、一般には 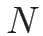 本の式であり、
よって
本の式であり、
よって 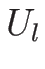 を任意に
を任意に 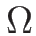 内のベクトルと固定し、
(4.25) から
内のベクトルと固定し、
(4.25) から 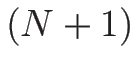 個の未知数である
個の未知数である
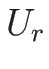 ,
, 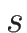 を求めると考えると、
それらは一つのパラメータで表現されるものとなり、
を求めると考えると、
それらは一つのパラメータで表現されるものとなり、
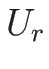 は相空間
は相空間 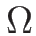 上の曲線 (曲線群) となるはずである。
この節では、それがどのようなものであるかを考えてみることにする。
ただし、一般の
上の曲線 (曲線群) となるはずである。
この節では、それがどのようなものであるかを考えてみることにする。
ただし、一般の 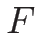 に対しては、
大域的な構造を知ることは無理なので、
ここでは
に対しては、
大域的な構造を知ることは無理なので、
ここでは 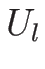 の近くに限定した局所的な構造を調べることになるが、
後で具体例で大域的な構造についても考える。
の近くに限定した局所的な構造を調べることになるが、
後で具体例で大域的な構造についても考える。
以後 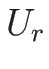 を、単に
を、単に 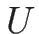 と書くことにする。
(4.25) の右辺を
と書くことにする。
(4.25) の右辺を
と変形し、この行列を
とすると、(4.25) は
![\begin{displaymath}
G(U)[U]=s[U]\end{displaymath}](img651.png) |
(4.75) |
と書ける。不連続線では ![$[U]\neq 0$](img652.png) なので、これは
なので、これは
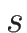 は
は 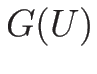 の固有値で、
の固有値で、![$[U]$](img653.png) はそれに対する固有ベクトル
はそれに対する固有ベクトル
であることを意味する。
であるので、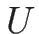 が
が 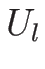 の十分近くにあれば、
の十分近くにあれば、
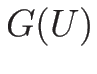 の固有方程式は
の固有方程式は
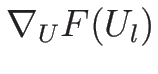 の固有方程式と近いものになり、
よって、両者の固有値、固有ベクトルも近いものとなる
(固有ベクトルの方は正確に言えば、近いものが取れる) ので、
の固有方程式と近いものになり、
よって、両者の固有値、固有ベクトルも近いものとなる
(固有ベクトルの方は正確に言えば、近いものが取れる) ので、
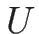 が
が 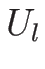 に十分近ければ、
に十分近ければ、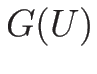 の固有値はすべて異なる実数で、
その固有値
の固有値はすべて異なる実数で、
その固有値 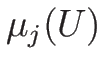 , およびそれに対する固有ベクトル
, およびそれに対する固有ベクトル 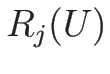 は、
は、
を満たす (ものが取れる)。
このとき (4.26) は、ある 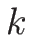 に対して、
に対して、
![\begin{displaymath}
s=\mu_k(U),\hspace{1zw}[U]\mathrel{/\!/}R_k(U)\end{displaymath}](img659.png) |
(4.76) |
を意味する。この後者の方程式
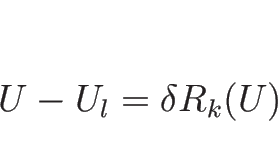 |
(4.77) |
によって相空間上の曲線
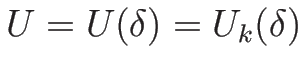 が得られ、
それによって
が得られ、
それによって 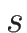 が
が
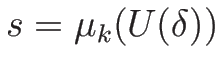 と
同じパラメータで表現されることになる。
と
同じパラメータで表現されることになる。
詳しく述べれば、
なので、陰関数定理により 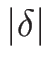 が十分小さいところで
が十分小さいところで
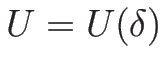 が一意に定まる。
よって、(4.28) は
が一意に定まる。
よって、(4.28) は  の近くで
確かに 1 本の相空間内の曲線
の近くで
確かに 1 本の相空間内の曲線 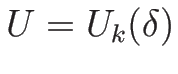 を決定し、
(4.26) は、
少なくとも
を決定し、
(4.26) は、
少なくとも 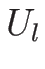 の近くでは
の近くでは  本の曲線
本の曲線
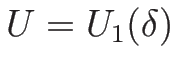 ,...
,...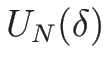 を与えることになる。
を与えることになる。
今度はもう少し細かく、その曲線 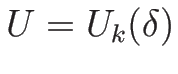 の向きや、
の向きや、
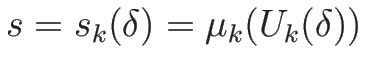 の変化について考えてみる。
まず (4.28) より、
の変化について考えてみる。
まず (4.28) より、
 のとき、
のとき、
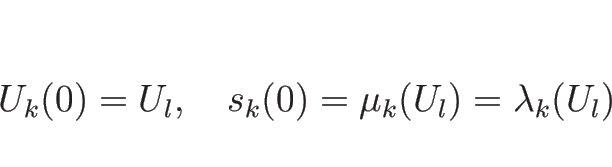 |
(4.78) |
となる。
また、(4.28) を 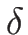 で微分すれば、
で微分すれば、
となるので、 とすれば
とすれば
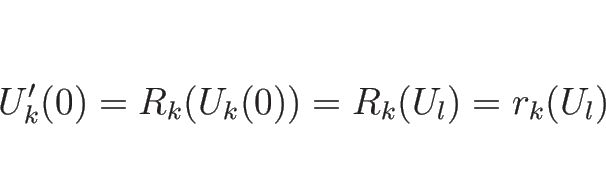 |
(4.79) |
が得られる。
次は 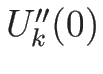 と
と 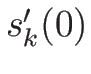 を求めるために、
(4.25) に戻って
を求めるために、
(4.25) に戻って
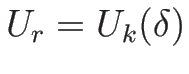 ,
,
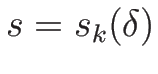 を代入して
を代入して 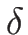 で 2 回微分する。
で 2 回微分する。
 とすると、(4.29), (4.30) より、
とすると、(4.29), (4.30) より、
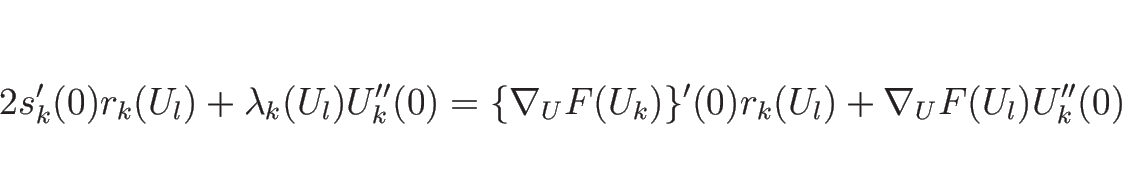 |
(4.80) |
となる。
一方、
に 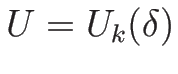 を代入して
を代入して 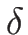 で微分すれば、
で微分すれば、
となるので、 とすると
とすると
となる。よって、(4.31) と
(4.32) の両辺を引き算して整理すると、
が得られる。
この (4.33) の両辺に、
左から左固有ベクトル 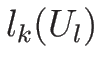 をかけると左辺が消え、
をかけると左辺が消え、
のみが残る。
補題 4.1
証明
より、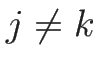 のときは
のときは
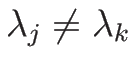 より
より
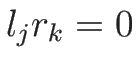 となる。
また、もしある
となる。
また、もしある 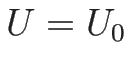 で
で
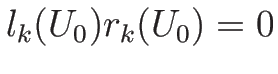 ならば、
ならば、
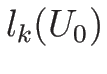 は
は 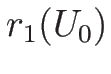 , ...
, ...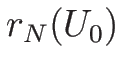 すべてと垂直であることになるが、
すべてと垂直であることになるが、
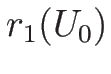 ,...
,...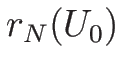 は一次独立なので、
それは
は一次独立なので、
それは 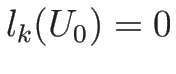 を意味してしまうので不合理。
よって
を意味してしまうので不合理。
よって 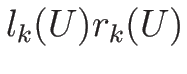 は、すべての
は、すべての 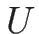 に対して 0 ではない。
に対して 0 ではない。
よって、この補題 4.1 により
となる。また、これを (4.33) に代入すれば、
より、この中括弧の部分は固有ベクトル、よって
となる。
結局、 での曲線
での曲線 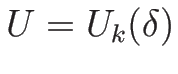 の方向、
の方向、
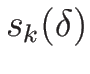 の増減については、
の増減については、
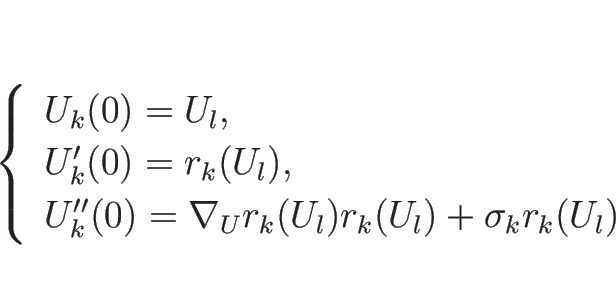 |
(4.83) |
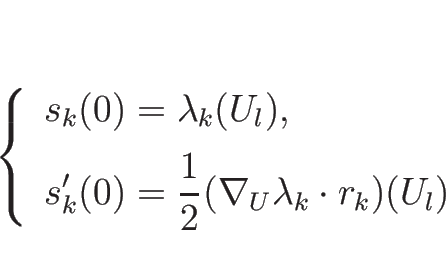 |
(4.84) |
が得られることになる。
補題 4.2
パラメータ 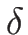 をとりかえることで、
(4.34) の
をとりかえることで、
(4.34) の 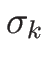 を 0 とすることができる。
を 0 とすることができる。
証明
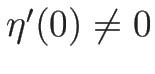 なる関数
なる関数 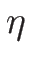 に対し
に対し
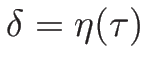 とすれば、
とすれば、
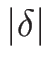 の十分小さいところでは
の十分小さいところでは 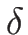 と
と 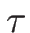 は 1 対 1 に対応
するので、パラメータ
は 1 対 1 に対応
するので、パラメータ 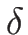 を
を 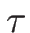 で置きかえることができる。
よって、そのようにとりえたものを
で置きかえることができる。
よって、そのようにとりえたものを 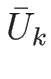 ,
, 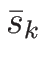 と
書くことにする:
と
書くことにする:
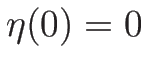 であれば
であれば
となる。また、
より、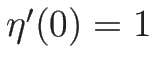 であれば 1 階微分の
であれば 1 階微分の 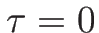 での値も変わらない。
での値も変わらない。
であるから、
なので、
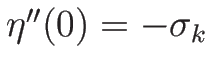 であれば、右辺は最初のものだけが残る。
よって、
であれば、右辺は最初のものだけが残る。
よって、
であれば、
が成り立つ。このような 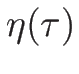 としては、例えば、
としては、例えば、
ととればよい (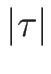 は十分小のとき)。
は十分小のとき)。
竹野茂治@新潟工科大学
2018-08-01
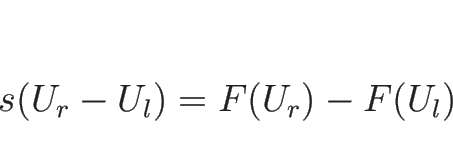
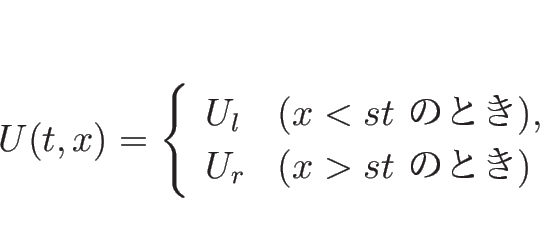
![]() 本の式であり、
よって
本の式であり、
よって ![]() を任意に
を任意に ![]() 内のベクトルと固定し、
(4.25) から
内のベクトルと固定し、
(4.25) から ![]() 個の未知数である
個の未知数である
![]() ,
, ![]() を求めると考えると、
それらは一つのパラメータで表現されるものとなり、
を求めると考えると、
それらは一つのパラメータで表現されるものとなり、
![]() は相空間
は相空間 ![]() 上の曲線 (曲線群) となるはずである。
この節では、それがどのようなものであるかを考えてみることにする。
ただし、一般の
上の曲線 (曲線群) となるはずである。
この節では、それがどのようなものであるかを考えてみることにする。
ただし、一般の ![]() に対しては、
大域的な構造を知ることは無理なので、
ここでは
に対しては、
大域的な構造を知ることは無理なので、
ここでは ![]() の近くに限定した局所的な構造を調べることになるが、
後で具体例で大域的な構造についても考える。
の近くに限定した局所的な構造を調べることになるが、
後で具体例で大域的な構造についても考える。
![]() を、単に
を、単に ![]() と書くことにする。
(4.25) の右辺を
と書くことにする。
(4.25) の右辺を
![\begin{displaymath}
F(U)-F(U_l)
=\Bigl[F(U_l+\tau(U-U_l)\Bigr]^{\tau=1}_{\tau=0}
=\int_0^1\nabla_UF(U_l+\tau(U-U_l))d\tau(U-U_l)
\end{displaymath}](img649.png)
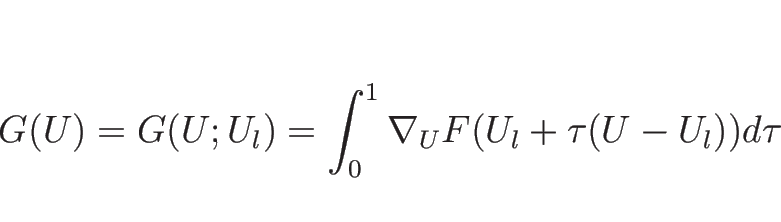
は
の固有値で、
はそれに対する固有ベクトル
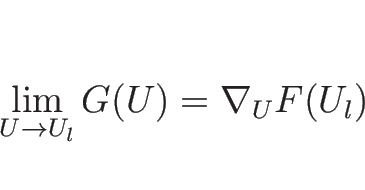
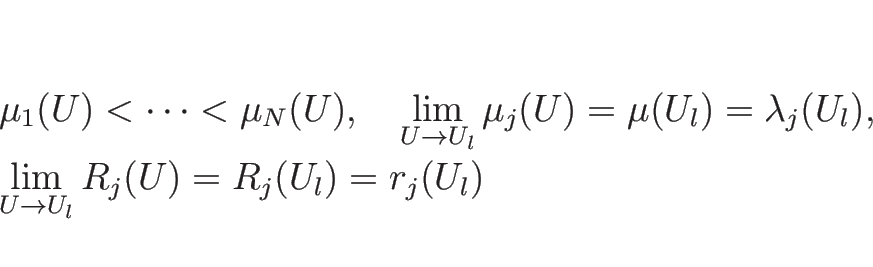
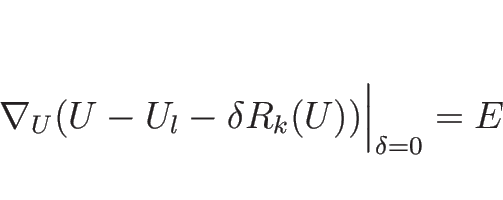
![]() の向きや、
の向きや、
![]() の変化について考えてみる。
まず (4.28) より、
の変化について考えてみる。
まず (4.28) より、
![]() のとき、
のとき、
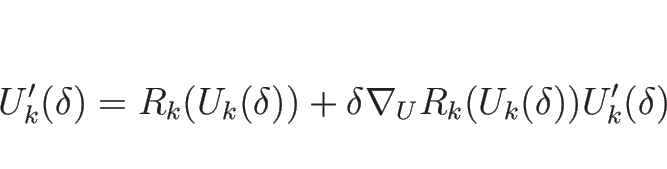
![]() と
と ![]() を求めるために、
(4.25) に戻って
を求めるために、
(4.25) に戻って
![]() ,
,
![]() を代入して
を代入して ![]() で 2 回微分する。
で 2 回微分する。
![\begin{eqnarray*}&&
s_k(\delta)(U_k(\delta)-U_l)=F(U_k(\delta))-F(U_l)
\\ &&
...
...k]+2s_k'U_k'+s_kU_k''=\{\nabla_UF(U_k)\}'U_k'+\nabla_UF(U_k)U_k''\end{eqnarray*}](img678.png)
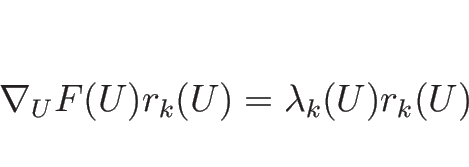
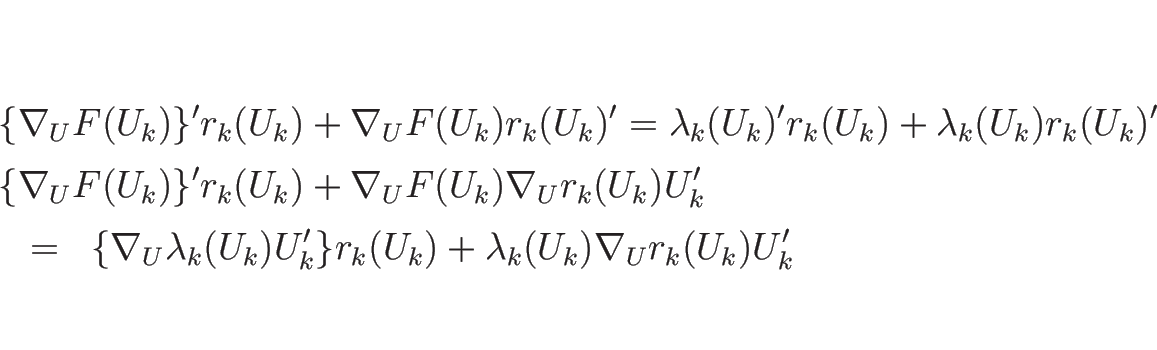
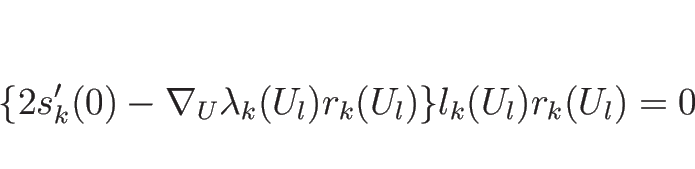
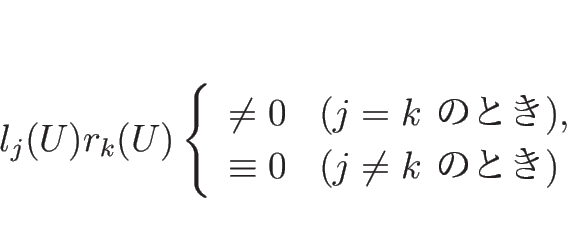
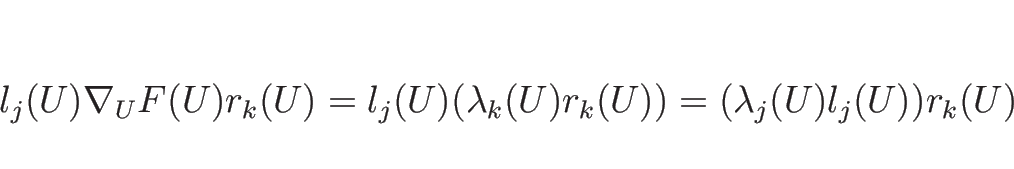
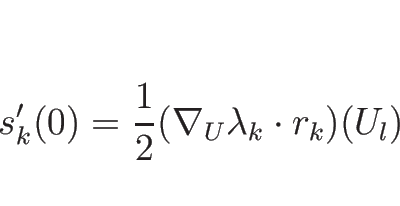
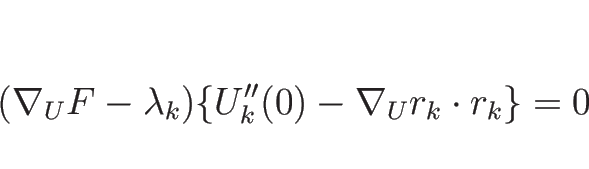
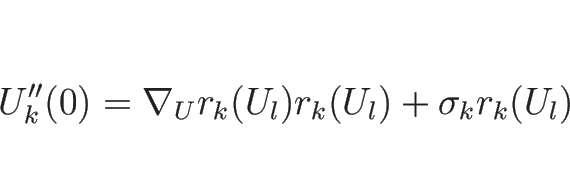
![]() での曲線
での曲線 ![]() の方向、
の方向、
![]() の増減については、
の増減については、
![]() をとりかえることで、
(4.34) の
をとりかえることで、
(4.34) の ![]() を 0 とすることができる。
を 0 とすることができる。
![]() なる関数
なる関数 ![]() に対し
に対し
![]() とすれば、
とすれば、
![]() の十分小さいところでは
の十分小さいところでは ![]() と
と ![]() は 1 対 1 に対応
するので、パラメータ
は 1 対 1 に対応
するので、パラメータ ![]() を
を ![]() で置きかえることができる。
よって、そのようにとりえたものを
で置きかえることができる。
よって、そのようにとりえたものを ![]() ,
, ![]() と
書くことにする:
と
書くことにする: