方程式 (3.3) は、スケール変換
![]() (
(![]() : 定数)
に関して不変、
すなわち
: 定数)
に関して不変、
すなわち ![]() が (3.3) の解であるとき、
が (3.3) の解であるとき、
![]() も (3.3) の解であり、
そのスケール変換に関して不変な初期値を与えれば、
そしてもしその初期値問題の解が一意的ならば、
も (3.3) の解であり、
そのスケール変換に関して不変な初期値を与えれば、
そしてもしその初期値問題の解が一意的ならば、
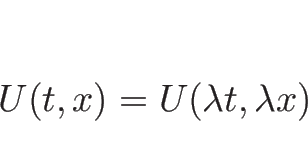
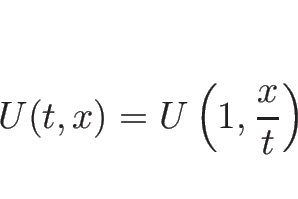
実際に、滑らかな中心波を求めてみることにする。
![]() を 1 変数
を 1 変数 ![]() の滑らかな関数で、
の滑らかな関数で、
![]() であるとすると、
であるとすると、
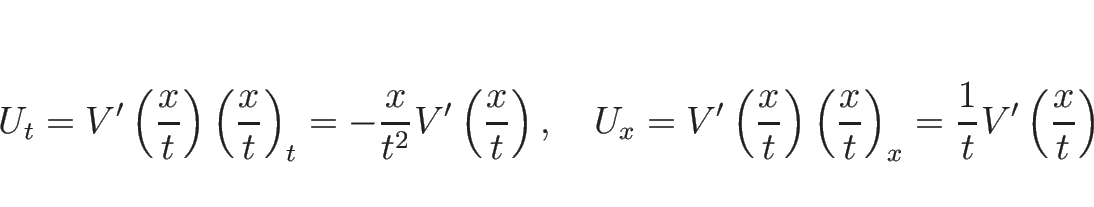
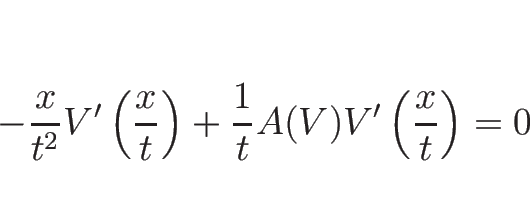
この式 (3.5) は 1 本の式、
(3.6) は ![]() 本の式で、
合計
本の式で、
合計 ![]() 本の式があることになるが、
未知関数はベクトル値関数
本の式があることになるが、
未知関数はベクトル値関数 ![]() とスカラー値関数
とスカラー値関数 ![]() 、
つまり
、
つまり ![]() 個の関数となるので、
この
個の関数となるので、
この ![]() 本の式でこれらが決定されることとなる。
本の式でこれらが決定されることとなる。
(3.6) の式は
![]() と
と ![]() が平行であることを表しているが、
ベクトル
が平行であることを表しているが、
ベクトル ![]() を
を ![]() 内のベクトル場と見れば、
(3.6) は
内のベクトル場と見れば、
(3.6) は
![]() がそのベクトル場の積分曲線であることを意味している。
よって、(3.6) の式は
がそのベクトル場の積分曲線であることを意味している。
よって、(3.6) の式は
![]() 内の
内の ![]() の軌道 (
の軌道 (![]() にはよらない) を決定し、
その軌道上のパラメータに関する依存性 (移動速度) を決定するのが
(3.5) であると見ることができる。
にはよらない) を決定し、
その軌道上のパラメータに関する依存性 (移動速度) を決定するのが
(3.5) であると見ることができる。
この、![]() の積分曲線
の積分曲線 ![]() 上での
上での ![]() の変化を
考えてみる。
(3.6) より、
の変化を
考えてみる。
(3.6) より、
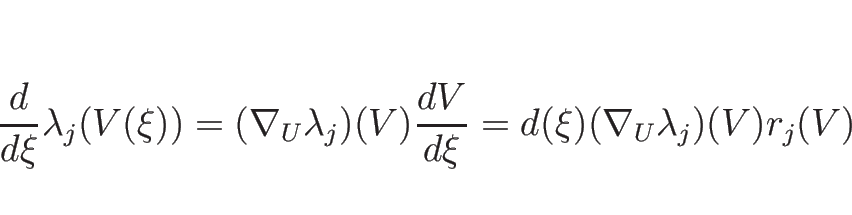
![]() で
で
![]() である場合は、
である場合は、
![]() -特性方向は 線形退化 (linearly degenerate) しているといい、
-特性方向は 線形退化 (linearly degenerate) しているといい、
![]() のすべての
のすべての ![]() で
で
![]() である場合は、
である場合は、![]() -特性方向は 真性非線形 (genuinely nonlinear)
であるという。
真性非線形の場合は、
必要ならば
-特性方向は 真性非線形 (genuinely nonlinear)
であるという。
真性非線形の場合は、
必要ならば ![]() の代わりに
の代わりに ![]() を考えることで、
を考えることで、
![]() と仮定することにする。
なお、
と仮定することにする。
なお、![]() をさらに正規化して、
をさらに正規化して、
![]() とすることも多い
(が、ここでは単に正であるとしておく)。
とすることも多い
(が、ここでは単に正であるとしておく)。
線形退化と真性非線形をごく特別な場合について説明する。
例えば ![]() が対角行列
が対角行列
![\begin{displaymath}
A(U)=\left[
\begin{array}{ccc}
\lambda_1(U) & & \smash{\lo...
...
\smash{\hbox{\Huge$0$}} && \lambda_N(U)
\end{array} \right]
\end{displaymath}](img250.png)
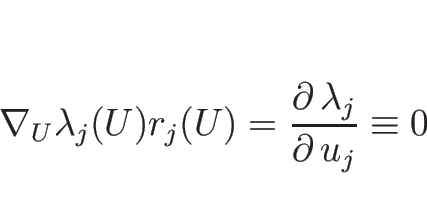
上に述べたように、![]() -特性方向が線形退化の場合は、この
-特性方向が線形退化の場合は、この ![]() に対して
(3.5), (3.6) を
満たす
に対して
(3.5), (3.6) を
満たす ![]() の形の解はないことになるが、
真性非線形の場合はその形の解が作られることがわかる。
その形の解を
の形の解はないことになるが、
真性非線形の場合はその形の解が作られることがわかる。
その形の解を ![]() -膨張波 (j-rarefaction wave) と呼ぶ。
-膨張波 (j-rarefaction wave) と呼ぶ。
![]() -膨張波解
-膨張波解 ![]() は、
は、
![]() (定数) という直線上では定ベクトル
(定数) という直線上では定ベクトル ![]() に等しく、
この直線は、(3.5) より
に等しく、
この直線は、(3.5) より
![]() であるので
であるので
![]() 、
すなわち
、
すなわち ![]() -特性曲線になっている。
なお一般に、(3.3) の解
-特性曲線になっている。
なお一般に、(3.3) の解 ![]() に対して、
に対して、
![]() 平面上の曲線
平面上の曲線 ![]() が
が ![]() -特性曲線 (
-特性曲線 (![]() -charcteristic curve)
であるとは、
-charcteristic curve)
であるとは、
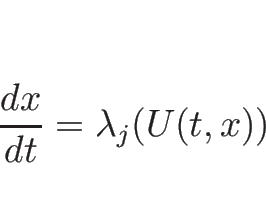
つまり、![]() -膨張波は、
-膨張波は、
ことが言える。-特性曲線がすべて (一点を通るような) 直線になっていて、 その直線上で
が一定であるような解であり、 それらの直線群の横断に対して、
は相空間
上でベクトル場
の積分曲線上を動く
![]() を一つ指定すると、
を一つ指定すると、![]() を通る
を通る ![]() に対する
積分曲線が一つ決まる。
その曲線の、
に対する
積分曲線が一つ決まる。
その曲線の、![]() から始まって
から始まって ![]() の増加する方向の
部分 (半曲線) を
の増加する方向の
部分 (半曲線) を ![]() -膨張波曲線 (
-膨張波曲線 (![]() -rarefaction wave curve)
と呼び、
-rarefaction wave curve)
と呼び、![]() と書く。
と書く。
定数ベクトルは (3.3) の解であるから、
単純な ![]() -膨張波解は、
-膨張波解は、
![]() に対して次の形の関数である:
に対して次の形の関数である:
この解 (3.8) は、
(3.3) のスケール変換不変な初期値
一般に、
![]() に対して、
(3.9) を初期値とする
(3.2) の初期値問題を
リーマン問題 (Riemann problem) という。
に対して、
(3.9) を初期値とする
(3.2) の初期値問題を
リーマン問題 (Riemann problem) という。
![]() とは限らない一般の
とは限らない一般の ![]() ,
, ![]() に対する
リーマン問題の解は、膨張波と不連続な解と定数ベクトルによって構成される。
に対する
リーマン問題の解は、膨張波と不連続な解と定数ベクトルによって構成される。
なお、上の膨張波解 (3.8) は、定数ベクトルや
膨張波自身は滑らかな関数 (![]() ) であるし、
定数ベクトルと膨張波の接続部分 (
) であるし、
定数ベクトルと膨張波の接続部分 (
![]() ,
,
![]() 上) では連続になっているが、
この接続部分では微分可能ではない。この微分可能性のない解や、
不連続な関数を解とみなすには、弱解という概念が必要となる。
これについては、4 章で説明する。
上) では連続になっているが、
この接続部分では微分可能ではない。この微分可能性のない解や、
不連続な関数を解とみなすには、弱解という概念が必要となる。
これについては、4 章で説明する。
竹野茂治@新潟工科大学