まずは、方程式 (4.1) の
導関数の不連続性について考える。
![]() が
が ![]() について連続で、
について連続で、
![]() 曲線
曲線 ![]() 以外ではなめらか (
以外ではなめらか (![]() ) で、
) で、
![]() では
では ![]() ,
, ![]() が不連続であるが、
が不連続であるが、
![]() への有限な極限値は存在する (第一種不連続) であるとする。
つまり、
への有限な極限値は存在する (第一種不連続) であるとする。
つまり、
まず、(4.10) を ![]() で微分すると、
で微分すると、
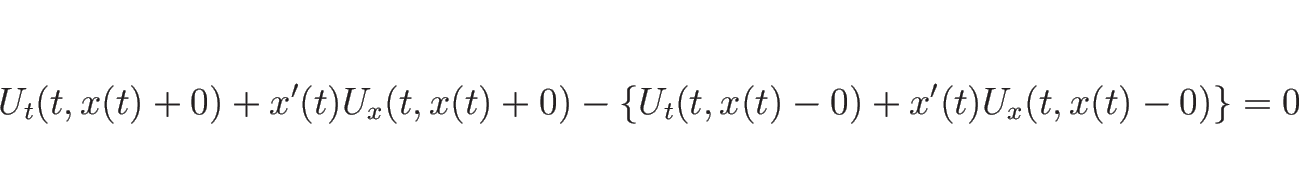
![\begin{displaymath}[U_t]=\Bigl[U_t\Bigr]^{x=x(t)+0}_{x=x(t)-0}
=-x'(t)[U_x]=-x'(t)H(t)
\end{displaymath}](img584.png)
![\begin{eqnarray*}[U_t]
&=&
[-F(U)_x]
=
-[\nabla_UF(U)U_x]
\\ &=&
-\nabla_U...
...x(t)))\{U_x(t,x(t)+0)-U_x(t,x(t)-0)\}
\\ &=&
-\nabla_UF(U) H(t)\end{eqnarray*}](img585.png)
例えば、膨張波解 (3.8) の端の特性曲線
![]() ,
,
![]() が、
この導関数の不連続線に相当する。
が、
この導関数の不連続線に相当する。
なお、[7] では、方程式を座標変換して考察しているが、
それはこの場合で言えば、この不連続線の近くで、
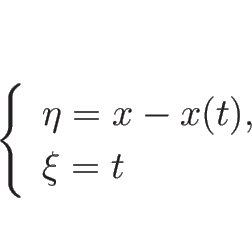
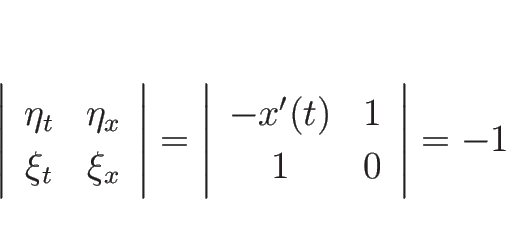
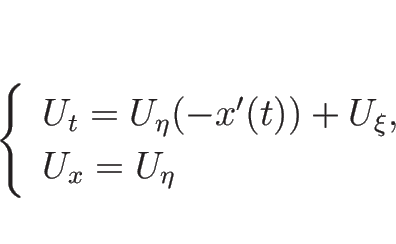
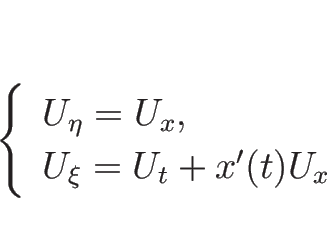
![\begin{eqnarray*}[U_\xi]
&=&
\frac{d}{d t}U(t,x(t)+0)-\frac{d}{d t}U(t,x(t)-0)=0,\\ [.5zh]
[U_\eta]
&=&
[U_x]=H(t)\end{eqnarray*}](img596.png)
よって、(4.1) を ![]() で表せば、
で表せば、
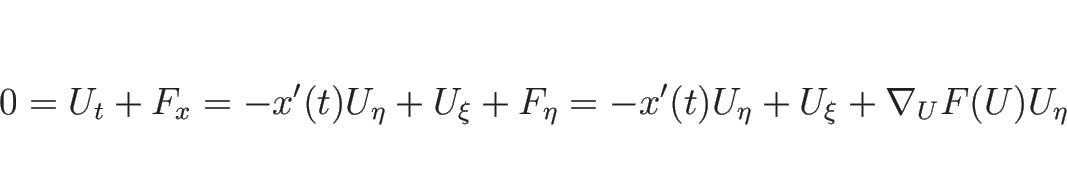
![\begin{displaymath}
-x'(t)[U_\eta]+[U_\xi]+\nabla_UF(U)[U_\eta]
=(\nabla_UF(U)-x'(t))H(t)
=0
\end{displaymath}](img598.png)
次は、![]() 自身の不連続性について考える。
そのために、2 節で微分方程式を導くために使われた
自身の不連続性について考える。
そのために、2 節で微分方程式を導くために使われた
![]() ,
, ![]() を考える。
を考える。
2.4 節では、
この ![]() ,
, ![]() に対する保存則
(2.9) を、それらが微分可能であるとして
に対する保存則
(2.9) を、それらが微分可能であるとして
![]() ,
, ![]() で微分することで質量保存則方程式 (2.10)
を導いたわけであるが、
今はその微分可能性を保証できない場合を考えるわけであるから、
むしろその前の、
で微分することで質量保存則方程式 (2.10)
を導いたわけであるが、
今はその微分可能性を保証できない場合を考えるわけであるから、
むしろその前の、![]() ,
, ![]() に対する保存則
(2.9) から始めるべきである。
に対する保存則
(2.9) から始めるべきである。
つまり一般には、(4.1) を考える代わりに、
その前の形の保存則として、
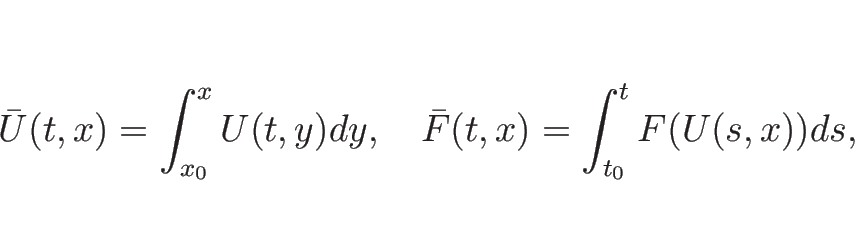
なめらか (![]() ) な曲線
) な曲線 ![]() が
が ![]() の不連続線で、
の不連続線で、
![]() はその左にあるとする。
この
はその左にあるとする。
この ![]() 以外では
以外では ![]() ,
, ![]() は十分滑らかで
(4.13) を満たし、
は十分滑らかで
(4.13) を満たし、
![]() では
では ![]() , は連続ではあるが、
その微分は不連続 (第一種不連続) であるとする:
, は連続ではあるが、
その微分は不連続 (第一種不連続) であるとする:
![\begin{displaymath}[\bar{F}]=-[\bar{U}]+[\bar{U}(t_0,x)]+[\bar{F}(t,x_0)]
=0
\end{displaymath}](img605.png)
(4.14) を ![]() について微分すると、
について微分すると、
![\begin{displaymath}[\bar{U}_t]+d'(t)[\bar{U}_x]=0
\end{displaymath}](img606.png)
![\begin{displaymath}[\bar{U}_t]=-d'(t)[U]
\end{displaymath}](img608.png)
![\begin{displaymath}[\bar{U}_t]
=
[-\bar{F}_t(t,x)+\bar{F}_t(t,x_0)]
=
-[\bar{F}_t(t,x)]
=
-[F]
\end{displaymath}](img609.png)
![\begin{displaymath}[F]=d'(t)[U]
\end{displaymath}](img610.png)
竹野茂治@新潟工科大学