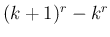
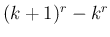 のような形の和がほとんどが消えて、
2 項だけが残ったからであるが、よって、もし
となるような関数
のような形の和がほとんどが消えて、
2 項だけが残ったからであるが、よって、もし
となるような関数 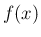 が見つかれば、
が見つかれば、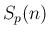 は、
は、
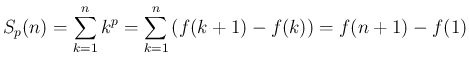
なお、本稿では、(5) を一つずらして、
さらに 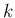 を一般の
を一般の 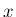 とした
とした
すべての 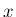 に対して (6) のような式を
満たす未知関数
に対して (6) のような式を
満たす未知関数 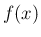 を求める問題は、一般に「差分方程式」と呼ばれる。
その差分方程式の解の性質を少し紹介するために、これを少し一般化した、
を求める問題は、一般に「差分方程式」と呼ばれる。
その差分方程式の解の性質を少し紹介するために、これを少し一般化した、
![$\displaystyle \left[f\right]_a^b = f(b)-f(a)
$](img30.png)
非斉次型の (7) の一般解 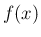 は、
(7) の解の一つ (「特殊解」と呼ばれる)
は、
(7) の解の一つ (「特殊解」と呼ばれる) 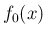 と、
周期 1 の任意の周期関数
と、
周期 1 の任意の周期関数 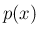 を用いて
を用いて
最初に、(8) の右辺で与えられる関数が、
確かに方程式 (7) を満たすことを示す。
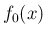 は (7) の特殊解なので、すべての
は (7) の特殊解なので、すべての 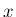 に対し
に対し
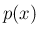 は周期 1 の周期関数なので
は周期 1 の周期関数なので 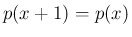 、よって
を満たす。(9), (10) より
、よって
を満たす。(9), (10) より
![$\displaystyle \left[f_0 +p\right]_{x-1}^x = \left[f_0\right]_{x-1}^x + \left[p\right]_{x-1}^x = g(x) + 0
$](img37.png)
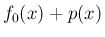 は (7) を満たすことがわかる。
次に、逆に (7) を満たす
は (7) を満たすことがわかる。
次に、逆に (7) を満たす 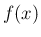 は
必ず
は
必ず 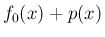 の形になることを示す。
(7) の任意の解を
の形になることを示す。
(7) の任意の解を 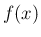 とすると、
とすると、
![$\displaystyle \left[f - f_0\right]_{x-1}^x = \left[f\right]_{x-1}^x - \left[f_0\right]_{x-1}^x = g(x) - g(x) = 0
$](img39.png)
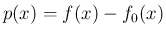 は
は 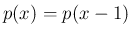 を
すべての
を
すべての  に対して満たすことになるから
に対して満たすことになるから  は周期 1 の周期関数
であることがわかる。
よって
は周期 1 の周期関数
であることがわかる。
よって 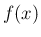 が (8) の右辺の形になることが示された。
が (8) の右辺の形になることが示された。
上の事実により、(7) の一般解を求めるには、
その特殊解 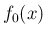 を求めればよいことになる。
なお、定数
を求めればよいことになる。
なお、定数 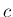 に対して
に対して
![$\displaystyle \left[f_0 + c\right]_{x-1}^x = \left[f_0\right]_{x-1}^x + \left[c\right]_{x-1}^x = \left[f_0\right]_{x-1}^x
$](img43.png)
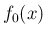 は
を満たすと仮定してよい (必要ならば
は
を満たすと仮定してよい (必要ならば 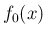 の代わりに
の代わりに 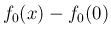 と
取ればよい)。
と
取ればよい)。
以後、0 以上の整数 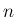 に対して、
に対して、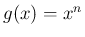 に対する
方程式 (7) の、
(11) を満たす特殊解を
に対する
方程式 (7) の、
(11) を満たす特殊解を 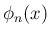 と書くことにする。
実は、このような
と書くことにする。
実は、このような 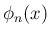 が
が 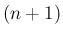 次多項式として
ただひとつ決まるのであるが、本節でそれを示す。
次多項式として
ただひとつ決まるのであるが、本節でそれを示す。
まず、そのような多項式があれば、それが多項式としては ただひとつの解であることはすぐにわかる。 それは、もし 2 つあったとすれば、 その差 (それも多項式) は上で見たように周期 1 の周期関数でなければならないが、 多項式の中で周期関数となるのは定数しかないので、その差は定数となり、 (11) の条件からその定数は 0 でなければならないからである。
よってあとはこの 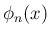 が存在することを示せばよいが、
本節では
が存在することを示せばよいが、
本節では 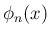 の漸化式を作ることで、それを構成的に示す。
の漸化式を作ることで、それを構成的に示す。
まず 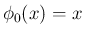 であることは容易にわかる。
今、そのような多項式
であることは容易にわかる。
今、そのような多項式
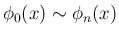
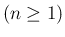 が
存在したとする。
方程式
が
存在したとする。
方程式
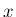 で微分すると、
で微分すると、
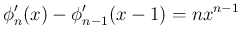
![$\displaystyle \left[\frac{\phi_n'}{n}\right]_{x-1}^x = x^{n-1}
$](img54.png)
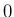 から
から 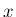 まで積分すれば
が得られるが、この
まで積分すれば
が得られるが、この
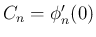 を
を 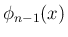 で
書き表すために (14) を (12) に代入すると、
で
書き表すために (14) を (12) に代入すると、
![$\displaystyle \left[\phi_n\right]_{x-1}^x
= n\left[\int_0^x\phi_{n-1}(t)dt + C_nx\right]_{x-1}^x
= n\int_{x-1}^x\phi_{n-1}(t)dt + nC_n
= x^n
$](img60.png)
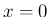 とすれば、
とすれば、
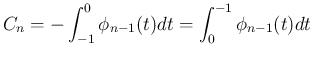
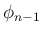 から
から 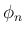 を求める漸化式
が得られる。
を求める漸化式
が得られる。
ただし、(15) はあくまでそのような多項式 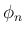 が
存在するとして導いたもので、
逆にそこから得られる
が
存在するとして導いたもので、
逆にそこから得られる 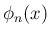 が
すべての
が
すべての 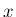 に対して (12) を満たすことはまだ保証されていない。
よって次は、(15) で得られる
に対して (12) を満たすことはまだ保証されていない。
よって次は、(15) で得られる 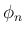 が、
確かに (12) と
が、
確かに (12) と 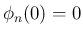 を満たすことを示す。
を満たすことを示す。
そこにも帰納的を用いる。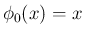 として、
として、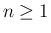 に対して、
に対して、
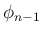 までは (12) と
までは (12) と 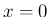 で 0 になることは
満たしていると仮定する。
で 0 になることは
満たしていると仮定する。
まず、
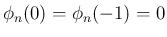 は、
(15) に
は、
(15) に 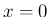 ,
, 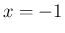 を代入すれば容易に得られる。
また、変数変換と帰納法の仮定により、
を代入すれば容易に得られる。
また、変数変換と帰納法の仮定により、
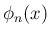 は、
(16) より、
は、
(16) より、
![\begin{eqnarray*}\left[\phi_n\right]_{x-1}^x
&=&
n\left[\int_0^x\phi_{n-1}(t)d...
...nt_{-1}^0\phi_{n-1}(t)dt
+ n\int_0^{-1}\phi_{n-1}(t)dt
\ =\ x^n\end{eqnarray*}](img77.png)
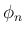 が (12) の解であることが
帰納的に保証されることになる。
が (12) の解であることが
帰納的に保証されることになる。
また、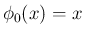 は 1 次式で、よって (15) に
より
は 1 次式で、よって (15) に
より 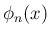 は多項式で、その次数は
は多項式で、その次数は 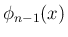 より
一つ上であることも帰納的に保証され、
よって
より
一つ上であることも帰納的に保証され、
よって 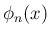 が
が 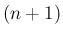 次式であることがわかる。
次式であることがわかる。
なお、(12) を 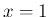 から
から 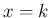 まで和を取れば、
まで和を取れば、
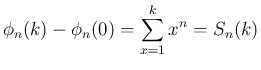
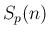 はこの
はこの 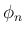 を用いて
と表される。以上により、通常は代数的に求める
を用いて
と表される。以上により、通常は代数的に求める 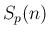 を、
解析的に積分を用いて求める漸化式 (15) が
得られたことになる。
を、
解析的に積分を用いて求める漸化式 (15) が
得られたことになる。
竹野茂治@新潟工科大学