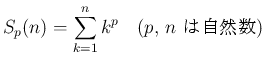 (1)
(1)
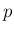 についてその公式を紹介している。
しかし大学で、この続きの公式を紹介することはまずないし、
実際にそれを用いることも多分ほとんどない。
についてその公式を紹介している。
しかし大学で、この続きの公式を紹介することはまずないし、
実際にそれを用いることも多分ほとんどない。
一方で、一般の自然数 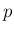 に対する (1) を
に対する (1) を 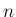 の式で
表す公式も知られていて、
「ファウルハーバーの公式」などと呼ばれることも
あるようである ([1]) が、
数学辞典 ([2]) では同様の式が「ベルヌーイ多項式」で
表されている。
の式で
表す公式も知られていて、
「ファウルハーバーの公式」などと呼ばれることも
あるようである ([1]) が、
数学辞典 ([2]) では同様の式が「ベルヌーイ多項式」で
表されている。
さらに「ファウルハーバーの定理」というもので
この 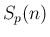 に関する性質も多少知られているようであるが、
Web 上にあるその説明 ([3]
に関する性質も多少知られているようであるが、
Web 上にあるその説明 ([3]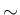 [8] 等) は、
代数的な計算の紹介やベルヌーイ数によるものが多いようだし、
高校の数学でも (2) は
[8] 等) は、
代数的な計算の紹介やベルヌーイ数によるものが多いようだし、
高校の数学でも (2) は 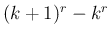 の展開式を
用いて代数的に導く計算で示されていると思う。
の展開式を
用いて代数的に導く計算で示されていると思う。
それに対し、本稿では「解析的」、すなわち微積分を用いて それを計算する方法を示し、 その「ファウルハーバーの定理」の性質も考察してみる。
竹野茂治@新潟工科大学