5 オイラー方程式の解
さて、微分方程式 (8) に戻ると、変数分離により、
となるので、この解は
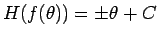 、すなわち、
、すなわち、
であることがわかる。
よって、これにより
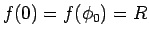 となるような解を作るには、
その 2 つのグラフをつながるようにつないで、
となるような解を作るには、
その 2 つのグラフをつながるようにつないで、
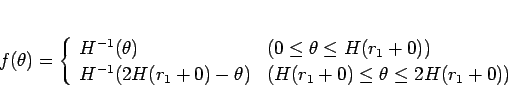 |
(14) |
とすればよい (図 4)。
あとは、この右端の 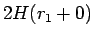 が
が 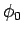 となるか、
すなわち
となるか、
すなわち 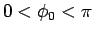 に対して、
に対して、
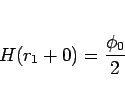 |
(15) |
となるような定数 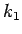 が常に一つ求まるかどうかを示せばよい。
が常に一つ求まるかどうかを示せばよい。
例えば、均質な (2) の場合には、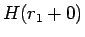 は
(11) であったから、
確かに
は
(11) であったから、
確かに 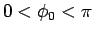 である任意の
である任意の 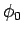 に対して
に対して
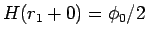 となる
となる 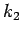 (
(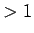 ) がただ一つ求まり、そこから
) がただ一つ求まり、そこから
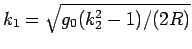 により
により 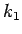 が求まってくれる。
が求まってくれる。
一般の 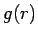 の場合にも、
次の命題 1 のように同様のことが成り立つことを示せる。
の場合にも、
次の命題 1 のように同様のことが成り立つことを示せる。
- 命題 1.
-
(12) の解
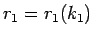 に対し、
に対し、
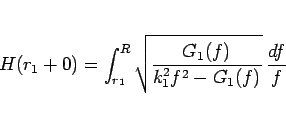 |
(16) |
を 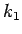 の関数
の関数 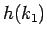 と見ると、
と見ると、
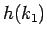 は
は 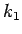 に関して増加関数であり、
に関して増加関数であり、
となる。
この命題 1 の証明は 8 節で行うが、
これにより
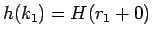 が
が 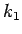 に関して
に関して 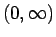 から
から 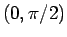 への 1 対 1 の関数であることになり、
よって (15) を満たす
への 1 対 1 の関数であることになり、
よって (15) を満たす 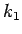 が任意の
が任意の 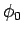 に
対して一つだけ求まることになる。
そしてそれによる (14) がオイラー方程式の解を与える。
に
対して一つだけ求まることになる。
そしてそれによる (14) がオイラー方程式の解を与える。
竹野茂治@新潟工科大学
2017年2月24日
![]() が
が ![]() となるか、
すなわち
となるか、
すなわち ![]() に対して、
に対して、
![]() は
(11) であったから、
確かに
は
(11) であったから、
確かに ![]() である任意の
である任意の ![]() に対して
に対して
![]() となる
となる ![]() (
(![]() ) がただ一つ求まり、そこから
) がただ一つ求まり、そこから
![]() により
により ![]() が求まってくれる。
が求まってくれる。
![]() の場合にも、
次の命題 1 のように同様のことが成り立つことを示せる。
の場合にも、
次の命題 1 のように同様のことが成り立つことを示せる。