3 変分法
次は (7) を最小にする関数 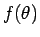 を変分法を用いて求める。
を変分法を用いて求める。
(7) の被積分関数を 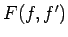 とすれば、
そのオイラー方程式 ([1] 参照) は
とすれば、
そのオイラー方程式 ([1] 参照) は
となる。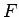 は
は 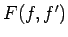 の形、すなわち陽には
の形、すなわち陽には 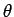 によらない形なので、
によらない形なので、
となり、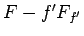 は定数となる。
は定数となる。
今の場合は、
となるので、よって 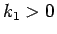 を定数として
を定数として
となる。変形すると、
なので、1 階の微分方程式
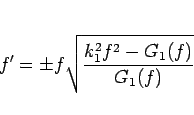 |
(8) |
が得られる。
良く知られているように、この微分方程式の解は、変数分離法により、
関数
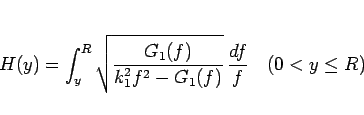 |
(9) |
の逆関数のようなものとして得られる。
竹野茂治@新潟工科大学
2017年2月24日
![]() とすれば、
そのオイラー方程式 ([1] 参照) は
とすれば、
そのオイラー方程式 ([1] 参照) は