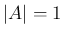
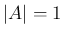 の直交行列
の直交行列 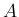 を軸回転行列で表現すること、
およびそのそれぞれの回転角を計算する方法について考察する。
を軸回転行列で表現すること、
およびそのそれぞれの回転角を計算する方法について考察する。
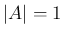 の直交行列
の直交行列
![$A=[\mbox{\boldmath$a$},\mbox{\boldmath$b$},\mbox{\boldmath$c$}]$](img99.png) は、
補題 3 により、(12) の形に
表すことができる。それを変形する。まずは
は、
補題 3 により、(12) の形に
表すことができる。それを変形する。まずは 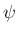 を外に出すと、
を外に出すと、
![\begin{eqnarray*}A
&=&
[\mbox{\boldmath$a$},\mbox{\boldmath$b$},\mbox{\boldma...
...-\mbox{\boldmath$\hat{p}$}]
A_x\left(\psi-\,\frac{\pi}{2}\right)\end{eqnarray*}](img294.png)
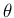 を外に出す。
を外に出す。
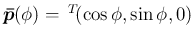 と書くと、
と書くと、
![$\displaystyle \mbox{\boldmath$p$}
=\left[\begin{array}{c}{\cos\phi\cos\theta}\\...
...ray}\right]
=\mbox{\boldmath$\bar{p}$}\sin\theta-\mbox{\boldmath$k$}\cos\theta
$](img296.png)
![\begin{eqnarray*}[\mbox{\boldmath$p$},\mbox{\boldmath$\check{p}$}, -\mbox{\boldm...
...p}$},\mbox{\boldmath$\check{p}$},\mbox{\boldmath$k$}]A_y(-\theta)\end{eqnarray*}](img297.png)
![$\displaystyle [\mbox{\boldmath$\bar{p}$},\mbox{\boldmath$\check{p}$},\mbox{\bol...
...{0}\\
{\sin\phi}&{\cos\phi}&{0}\\
{0}&{0}&{1}\end{array}\right]
=A_z(\phi)
$](img298.png)
なお、(42) では、3 軸すべての方向の回転が
使われているが、直交行列 (回転変換) の軸回転行列による表現としては、
2 軸 (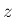 -
-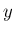 -
-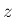 ,
, 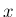 -
-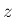 -
-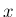 など) だけの形も
良く使われている。そのような形にするには、最初の式を変えればよい。
など) だけの形も
良く使われている。そのような形にするには、最初の式を変えればよい。
すなわち、
![$A=[\mbox{\boldmath$a$},\mbox{\boldmath$b$},\mbox{\boldmath$c$}]$](img99.png) は、
は、
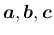 が右手系の正規直交系なので、
が右手系の正規直交系なので、
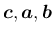 も右手系の正規直交系となるから、
補題 3 により、
も右手系の正規直交系となるから、
補題 3 により、
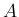 を
を 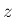 -
-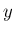 -
-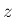 の 2 軸の回転で表現できることになる。
の 2 軸の回転で表現できることになる。
この角の計算可能性については、
例えば後者の 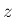 -
-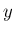 -
-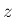 の回転の方で考えると、
(43) の
の回転の方で考えると、
(43) の
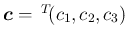 から、
から、
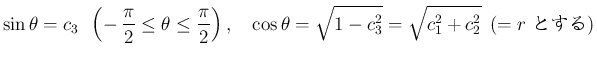
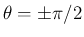 なら
なら 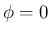 、
、
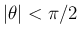 なら
なら
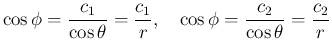
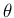 ,
, 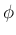 は
は
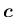 で決定する。
で決定する。
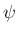 は、
は、
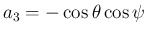 ,
,
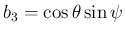 なので、
なので、
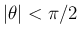 なら
と求まる。よってこの場合、
軸回転行列も
なら
と求まる。よってこの場合、
軸回転行列も 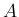 の成分を用いて以下のように表される。
の成分を用いて以下のように表される。
![\begin{eqnarray*}A_z(\phi)
&=&
\left[\begin{array}{ccc}{\cos\phi}&{-\sin\phi}&...
...r}&{0}\\
{b_3/r}&{-a_3/r}&{0}\\
{0}&{0}&{1}\end{array}\right]\end{eqnarray*}](img313.png)
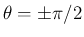 の場合は、
の場合は、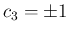 で
で
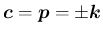 , よって
, よって 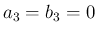 で、
で、
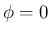 より
より
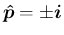 ,
,
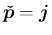 となり、
となり、
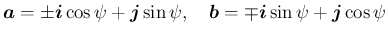
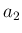 ,
, 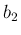 から
から 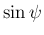 ,
, 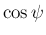 を
求めることができる。この場合、
を
求めることができる。この場合、
![\begin{eqnarray*}A_z(\phi)
&=&
A_z(0) \ =\ E,
\\
A_y\left(\frac{\pi}{2}\,-...
...&{-a_2}&{0}\\
{a_2}&{b_2}&{0}\\
{0}&{0}&{1}\end{array}\right]\end{eqnarray*}](img320.png)
竹野茂治@新潟工科大学