4 一般の指数関数
一般の正の実数 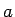 (
(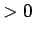 ) の実数乗「
) の実数乗「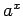 」に相当する
」に相当する
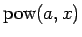 を、
を、
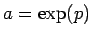 となる
となる 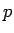 に対し、
に対し、
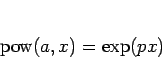 |
(28) |
と定義する。
まず、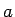 に対する
に対する 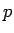 の存在であるが、
3 節、および (26) でみたように、
の存在であるが、
3 節、および (26) でみたように、
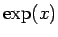 は増加関数で、(21) より
実数全体から正の実数全体への 1 対 1 の対応を与える。よって、
は増加関数で、(21) より
実数全体から正の実数全体への 1 対 1 の対応を与える。よって、
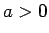 であれば
であれば 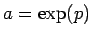 となる
となる 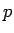 が必ず存在し、
かつただ一つ定まることがわかる。
が必ず存在し、
かつただ一つ定まることがわかる。
なお、この 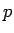 は
は 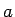 に対してただ一つ定まるので、
そのような
に対してただ一つ定まるので、
そのような 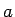 から
から 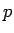 への対応を
への対応を 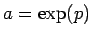 の逆関数と呼び、
通常は
の逆関数と呼び、
通常は
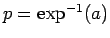 のように書くが、
のように書くが、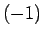 乗とまぎらわしいので、
本稿ではこれを
乗とまぎらわしいので、
本稿ではこれを 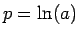 と書くことにする。
これにより、(28) は、
と書くことにする。
これにより、(28) は、
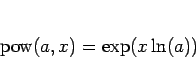 |
(29) |
と書けることになるが、これは (2) に対応する。
この (28) により、任意の 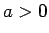 ,
, 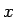 に対して
に対して 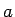 の
の 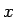 乗に相当する
乗に相当する
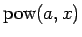 が定義されることになる。
が定義されることになる。
なお、 の場合を考えると、
の場合を考えると、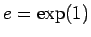 とすれば、
とすれば、
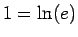 であるから
であるから
となるので、よって 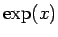 自身もこの意味で
「
自身もこの意味で
「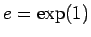 の
の 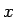 乗」に相当するものになっている。
乗」に相当するものになっている。
今度はこの
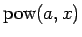 の性質を見ていく。
まず、(28) より、
の性質を見ていく。
まず、(28) より、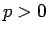 ならば
ならば
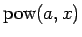 は増加関数、
は増加関数、
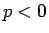 ならば
ならば
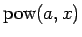 は減少関数であることがわかるが、
は減少関数であることがわかるが、
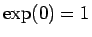 より、
より、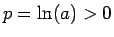 となるのは
となるのは 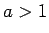 のとき、
のとき、
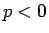 となるのは
となるのは 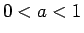 のときなので、
よって (21) より
のときなので、
よって (21) より
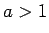 のときは
のときは
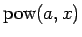 は増加関数で、
は増加関数で、
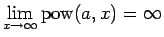 ,
,
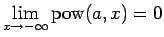
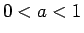 のときは
のときは
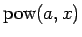 は減少関数で、
は減少関数で、
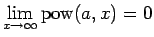 ,
,
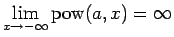
の単調性と漸近性が得られる。また、
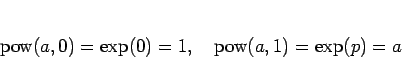 |
(30) |
も言える。
よって、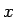 が正の有理数
が正の有理数 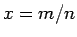 (
(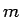 ,
, 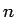 は自然数) であれば、
(24) より
は自然数) であれば、
(24) より
で、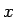 が負の有理数
が負の有理数 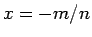 であれば、
であれば、
となり、確かに 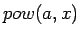 が通常の「
が通常の「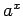 」に対応したもの、
すなわち通常の有理数乗を含んでいることがわかる。
」に対応したもの、
すなわち通常の有理数乗を含んでいることがわかる。
また、(25), (27) より、
の通常の指数法則 (
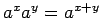 ,
,
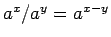 ) が
成り立つこともわかる。
) が
成り立つこともわかる。
次は、
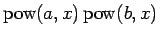 を考える。
を考える。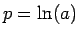 ,
, 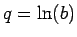 とすると、
とすると、
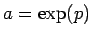 ,
, 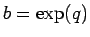 であるから、
であるから、
となるので、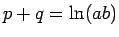 であり、よって、
であり、よって、
の指数法則 (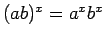 ) が成り立つ。
同様にして、
) が成り立つ。
同様にして、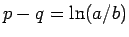 より
より
となること (
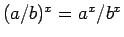 ) も示される。
) も示される。
最後に「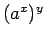 」の指数法則、すなわち
」の指数法則、すなわち
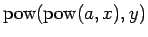 であるが、
であるが、
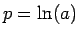 ,
,
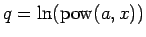 とすると、
とすると、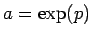 ,
,
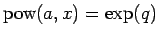 となるが、
となるが、
より 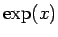 の単調性から
の単調性から 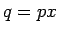 である。よって、
である。よって、
となり、「
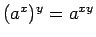 」に対応するものが得られる。
」に対応するものが得られる。
竹野茂治@新潟工科大学
2017年2月2日
![]() は
は ![]() に対してただ一つ定まるので、
そのような
に対してただ一つ定まるので、
そのような ![]() から
から ![]() への対応を
への対応を ![]() の逆関数と呼び、
通常は
の逆関数と呼び、
通常は
![]() のように書くが、
のように書くが、![]() 乗とまぎらわしいので、
本稿ではこれを
乗とまぎらわしいので、
本稿ではこれを ![]() と書くことにする。
これにより、(28) は、
と書くことにする。
これにより、(28) は、
![]() の場合を考えると、
の場合を考えると、![]() とすれば、
とすれば、
![]() であるから
であるから
![]() の性質を見ていく。
まず、(28) より、
の性質を見ていく。
まず、(28) より、![]() ならば
ならば
![]() は増加関数、
は増加関数、
![]() ならば
ならば
![]() は減少関数であることがわかるが、
は減少関数であることがわかるが、
![]() より、
より、![]() となるのは
となるのは ![]() のとき、
のとき、
![]() となるのは
となるのは ![]() のときなので、
よって (21) より
のときなので、
よって (21) より
![]() を考える。
を考える。![]() ,
, ![]() とすると、
とすると、
![]() ,
, ![]() であるから、
であるから、
![]() 」の指数法則、すなわち
」の指数法則、すなわち
![]() であるが、
であるが、
![]() ,
,
![]() とすると、
とすると、![]() ,
,
![]() となるが、
となるが、