2.5 運動量保存則

2.4 節と同様に、今度は運動量保存則について考える。

2.2 節で 質量に対して $M^1$, $N^1$, $\bar{M}^1$, $\bar{N}^1$ のように書いたものを、 質量を運動量で置き換えたものを $M^2$, $N^2$, $\bar{M}^2$, $\bar{N}^2$ のように書くことにする。それを局所化したものを、 ここでは $m(t,x)$, $Q(t,x)$ と書くことにする。すなわち、

$$m(t,x) = \mbox{$(t,x)$\ での単位長さあたりの運動量 }$$

$$= \lim_{\Delta x\rightarrow +0} \frac{M^2_{[x,x+\Delta x]}(t)}{\Delta x} = \frac{\partial\, \bar{M}^2}{\partial\, x},$$ (2.11)

$$Q(t,x) = \mbox{$(t,x)$\ での単位時間あたりでの運動量通過量 }$$

$$= \lim_{\Delta t\rightarrow +0} \frac{N^2_{[t,t+\Delta t]}(x)}{\Delta t} = \frac{\partial\, \bar{N}^2}{\partial\, t}$$ (2.12)

とする。

運動量は質量と速度の積なので、 $\Delta x\approx 0$ のとき

$$M^2_{[x,x+\Delta x]}(t)\approx M^1_{[x,x+\Delta x]}(t)u(t,x)$$

となる。よって、この両辺を $\Delta x$ で割って $\Delta x\rightarrow +0$ とすれば、両辺の誤差は 0 に収束し、

$$m(t,x)=\rho(t,x)u(t,x)$$ (2.13)

が得られる。

2.3 節の (2.6) の関係式は、 そのまま $N^1$, $M^1$ を $N^2$, $M^2$ に 置き換えたものが成立し、その後の議論もそのまま成立する。 よって、この場合 (2.7) に変わって

$$Q(t,x)=m(t,x)u(t,x)=\rho(t,x) (u(t,x))^2$$ (2.14)

が得られる。

$a\leq x\leq b$, $c\leq t\leq d$ での運動量の変化を考えると、 それは運動量の流入と流出だけではなく力積も追加されるので、

$$M^2_{[a,b]}(d)-M^2_{[a,b]}(c)=N^2_{[c,d]}(a)-N^2_{[c,d]}(b)+K$$

となる。 ここで $K$ は、この部分の気体にこの時間内に与えられた力積の総量であり、 (2.8) とはその点のみが異なる。

もし、この気体には力としては圧力しか働いていない (つまり外力はない) とすると、 $P(t,x)$ を時刻 $t$ のときに $x$ での断面全体で左右に向く気体の圧力とすれば、 圧力はどの方向にも等しく働くスカラー量であるから、 $a<x<b$ の内部では圧力による力積は左右分が打ち消されるので 0 であり、 よって境界で働く圧力のみがこの内部の運動量の増減に関係する。 力積は、力と時間の積で得られるので、結局 $K$ は

$$K=\int_c^d P(t,a)dt-\int_c^d P(t,b)dt$$

と書けることになる。 よって、2.4 節と同様に $(a,b,c,d)=(x_0,x,t_0,t)$ とすれば、

$$\bar{M}^2(t,x)+\bar{N}^2(t,x) =\bar{M}^2(t_0,x)+\bar{N}^2(t,x_0) +\int_{t_0}^t P(s,x_0)ds-\int_{t_0}^t P(s,x)ds$$

となり、これを $t$, $x$ で微分すれば、(2.11), (2.12) より、

$$m_t+Q_x =\frac{\partial^2}{\partial t\partial x}\int_{t_0}^t\{P(s,x_0)-P(s,x)\}ds =-P(t,x)_x$$

となる。よって、(2.13), (2.14) より、 運動量保存則を表す方程式

$$(\rho u)_t+(\rho u^2+P)_x=0$$ (2.15)

が得られる。

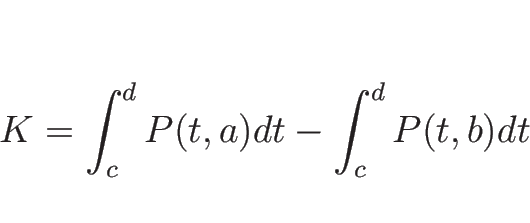
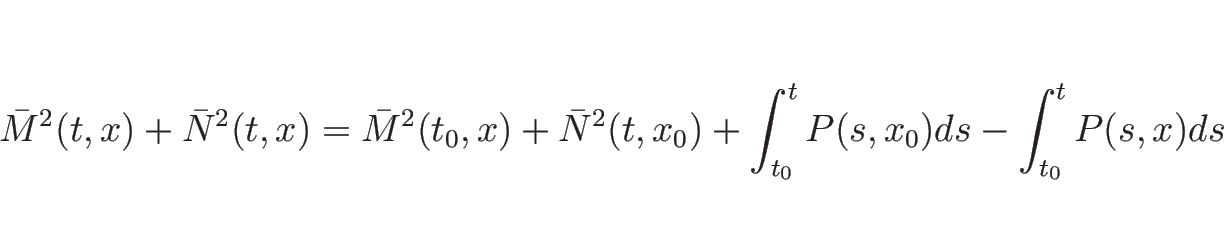
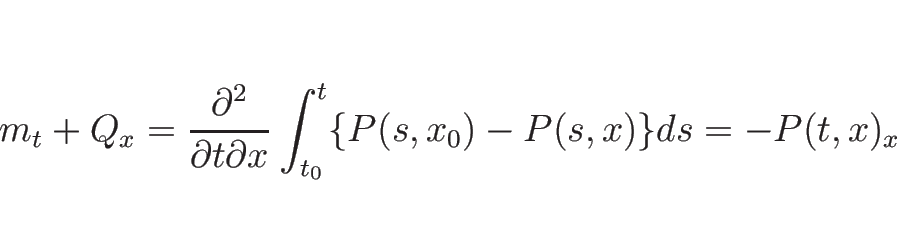
エネルギー保存則も同様に考えることができ、 エネルギー密度を $E$ とすれば、 運動量の場合に境界からの追加が力積であった部分が、 エネルギーの場合は境界から仕事量として

$$\int_c^d P(t,a)u(t,a)dt-\int_c^d P(t,b)u(t,b)dt$$

の式で追加されるので、

$$E_t+(Eu+Pu)_x=0$$

となる。$E$ は、気体粒子の運動エネルギーと、 気体粒子の持つ内部エネルギーの和であり、 単位質量あたりの内部エネルギーを $e=e(\rho,P)$ とすると

$$E=\frac{1}{2}\rho u^2+\rho e$$

と書ける。よって、エネルギー保存則は、

$$\left(\frac{1}{2}\rho u^2+\rho e\right)_t +\left\{\left(\frac{1}{2}\rho u^2+\rho e+P\right)u\right\}_x=0$$ (2.16)

となる。$e$ は、理想気体では標準的に

$$e=\frac{P}{(\gamma-1)\rho}$$ (2.17)

という式が使われるようであり、 ここで $\gamma$ は $1<\gamma<3$ の定数である。

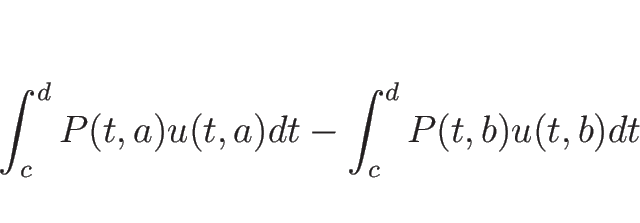
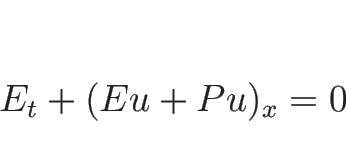
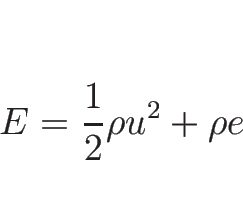
この (2.10), (2.15), (2.16) の 3 本の連立微分方程式が、 1 次元の理想気体の基礎的な保存則方程式系であり、 この場合未知関数は、$(\rho,m,E)$ や $(\rho,u,P)$ などと考えて 考察することになる。

また、圧力 $P$ が密度 $\rho$ のみによって決定するバロトロピー流 ($P=P(\rho)$、例えば等エントロピー流: $P=A\rho^\gamma$, 等温流: $P=A\rho$ など) であるという仮定を置いて、 エネルギー保存則 (2.16) を除いた (2.10), (2.15) の 2 本 だけで考察することもよく行われる。この場合は、 $(\rho,m)$ や $(\rho ,u)$ を未知関数と考える。