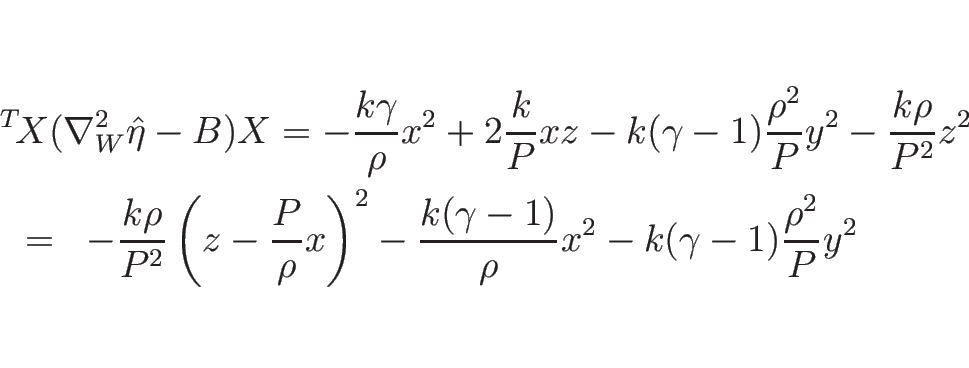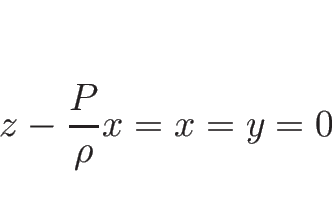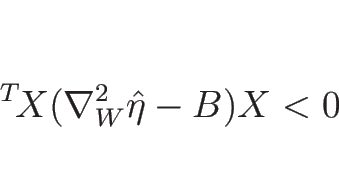B.4 物理的なエントロピーの凹性
最後に、B.3 節で述べた、
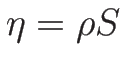 の
の
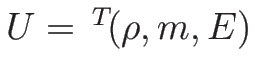 での凹性について述べておく。
での凹性について述べておく。
この 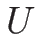 に関する 2 階微分による行列
に関する 2 階微分による行列
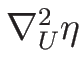 を
計算するわけであるが、
この行列の計算は、これまでのように
を
計算するわけであるが、
この行列の計算は、これまでのように
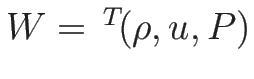 で
行えばよい、とはいかない。
まずは、そこから検証する。
で
行えばよい、とはいかない。
まずは、そこから検証する。
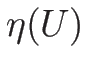 に
に 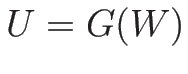 を代入したものを
を代入したものを
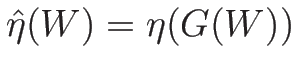 と
すると、
と
すると、
であり、また、
であるから、
となる。
今、 行列
行列 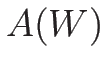 と定数列ベクトル (
と定数列ベクトル (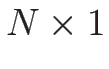 行列)
行列) 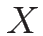 に
対し、
に
対し、
という 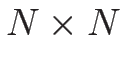 行列となるが、これを記号的に
行列となるが、これを記号的に
と書くことにする
(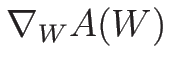 は、単独では意味のない記号になってしまうので、
特にこのように書くこととする)。
こうすれば、
は、単独では意味のない記号になってしまうので、
特にこのように書くこととする)。
こうすれば、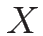 も
も 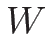 の関数
の関数 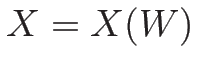 である場合も
である場合も
のように、積の微分の形に書くことができる。
この記法により、
となるが、
なので、よって、
となる。
今、右辺の最初の行列を
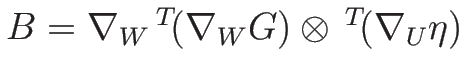 とすると、
とすると、
となるので、
となる。よって、
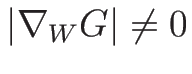 であるから、
であるから、
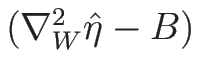 が正定値 (負定値) であることと、
が正定値 (負定値) であることと、
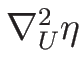 が正定値 (負定値) であることは同値となる。
ただし、一般には
が正定値 (負定値) であることは同値となる。
ただし、一般には 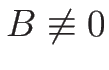 なので、
なので、
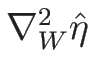 と
と
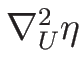 が対応するわけではない。
が対応するわけではない。
今度は、
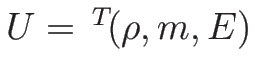 ,
,
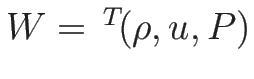 に対して
に対して
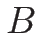 を計算してみる。
を計算してみる。
であり、また定義より
であり、
となる。
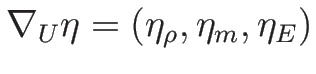 なので、よって、
なので、よって、
となる。ここで、
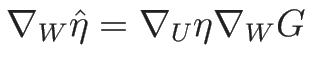 より、
より、
なので、
となり、よって 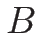 を
を 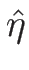 で表わせば、
で表わせば、
となる。
次に、具体的な
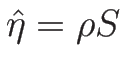 に対して、
に対して、
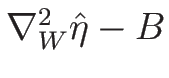 を求める。
(B.3) より、
を求める。
(B.3) より、
と書けるから、
となり、よって、
となり、よって、
となる。
今、
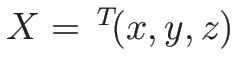 に対して、
に対して、
となるので、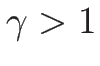 より、これは確かに 0 以下で、
しかもこれが 0 になるのは
より、これは確かに 0 以下で、
しかもこれが 0 になるのは
となるときのみで、これは 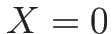 を意味するから、結局、
を意味するから、結局、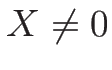 ならば
ならば
であることが言え、
よって
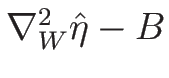 が負定値であることが言える。
ゆえに
が負定値であることが言える。
ゆえに
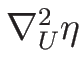 は負定値となり、
は負定値となり、
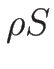 が凹であることが言える。
が凹であることが言える。
竹野茂治@新潟工科大学
2018-08-01
![]() に関する 2 階微分による行列
に関する 2 階微分による行列
![]() を
計算するわけであるが、
この行列の計算は、これまでのように
を
計算するわけであるが、
この行列の計算は、これまでのように
![]() で
行えばよい、とはいかない。
まずは、そこから検証する。
で
行えばよい、とはいかない。
まずは、そこから検証する。
![]() に
に ![]() を代入したものを
を代入したものを
![]() と
すると、
と
すると、
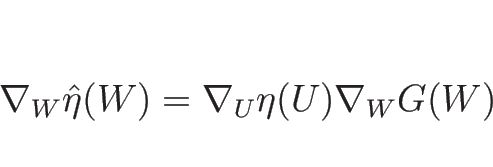
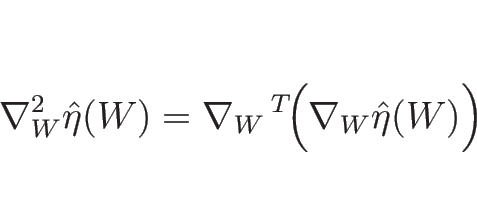
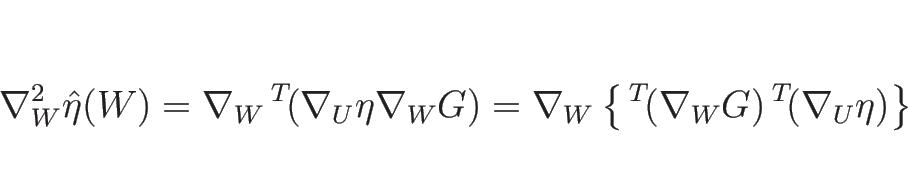
![]() 行列
行列 ![]() と定数列ベクトル (
と定数列ベクトル (![]() 行列)
行列) ![]() に
対し、
に
対し、
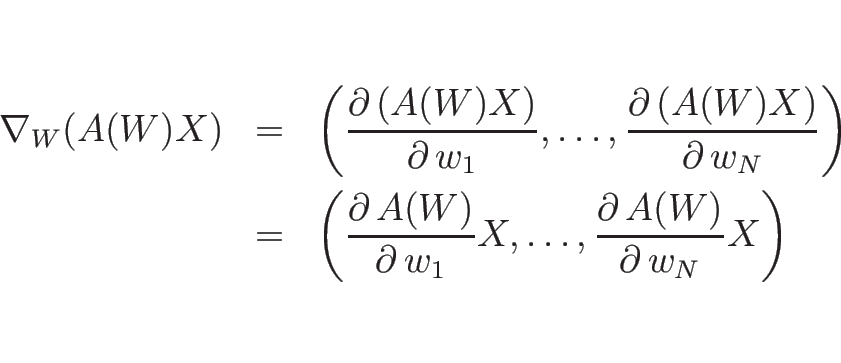
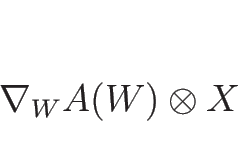
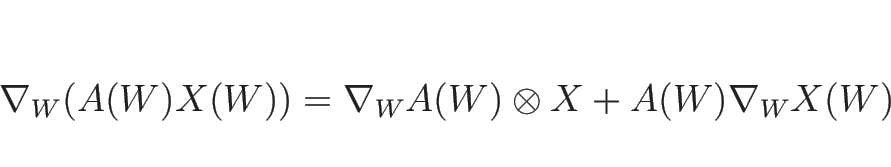
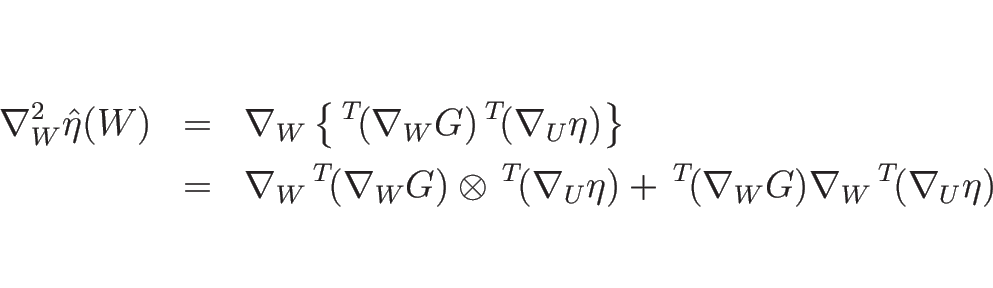
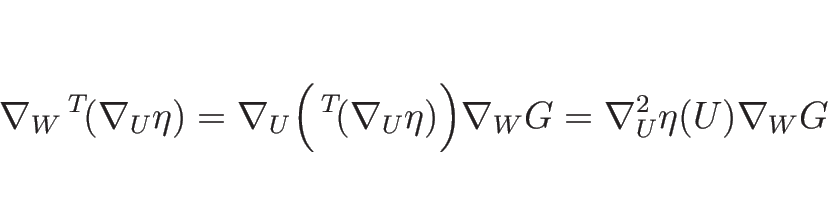
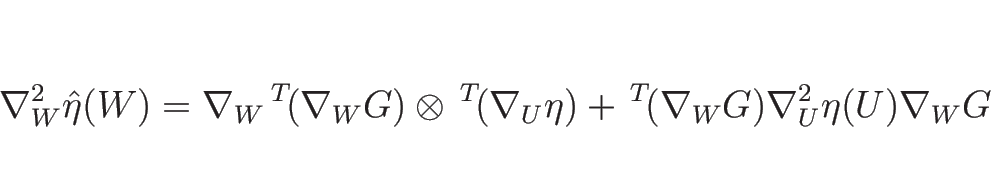
![]() とすると、
とすると、
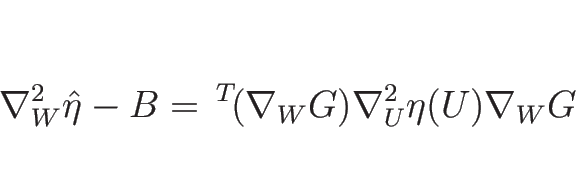
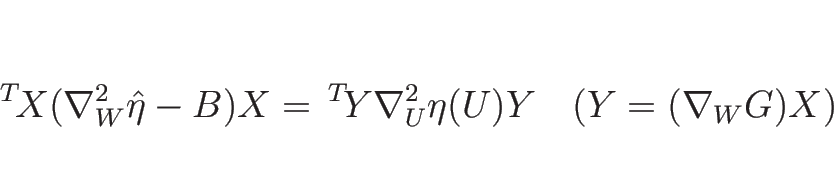
![]() ,
,
![]() に対して
に対して
![]() を計算してみる。
を計算してみる。
![\begin{displaymath}
\nabla_W G
=\left(\frac{\partial\, }{\partial\, \rho},\frac{...
...rho & 0 \\
u^2/2 & \rho u & 1/(\gamma-1)
\end{array}\right]
\end{displaymath}](img1438.png)
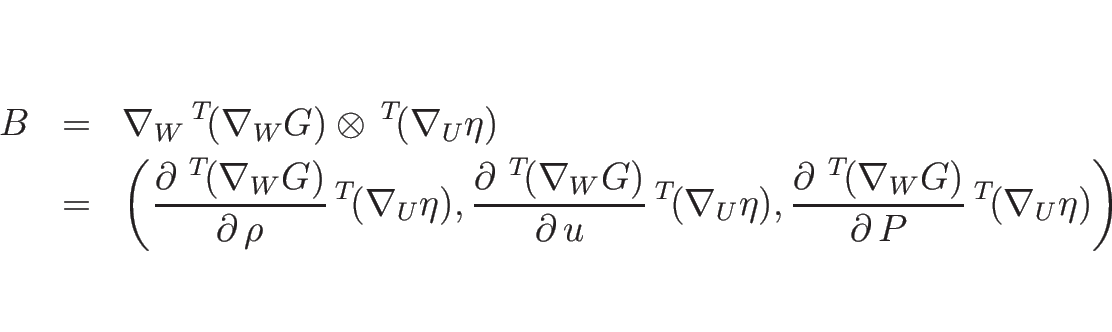
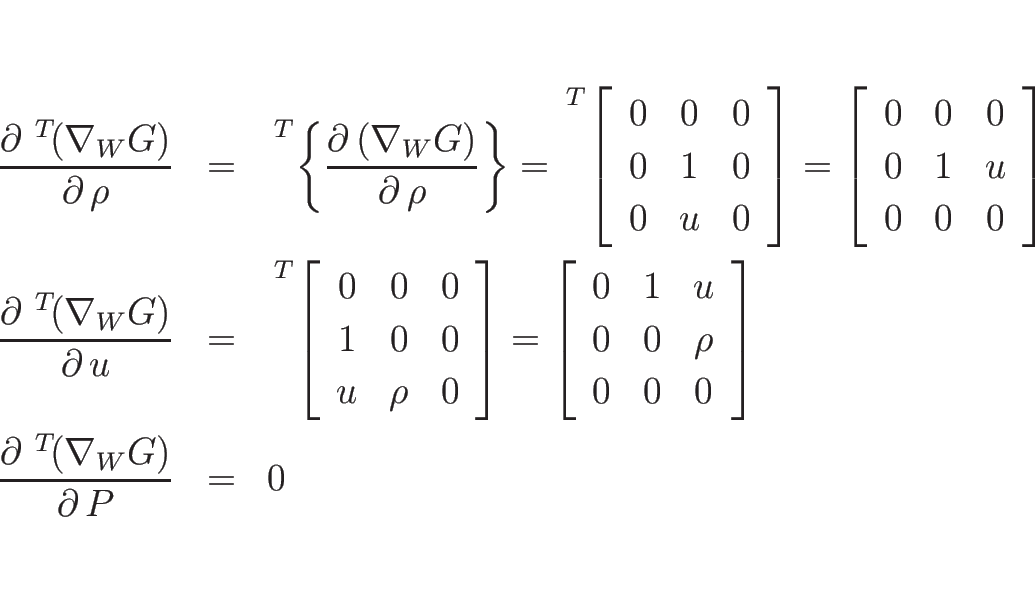
![\begin{displaymath}
B=\left[\begin{array}{ccc}
0 & \eta_m+u\eta_E & 0\\
\eta_m+u\eta_E & \rho\eta_E & 0 \\
0 & 0 & 0
\end{array}\right]
\end{displaymath}](img1442.png)
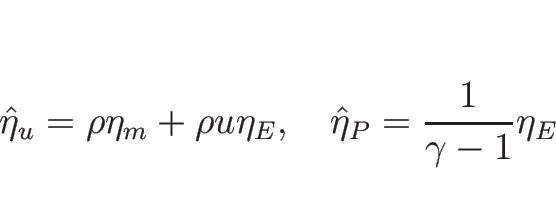
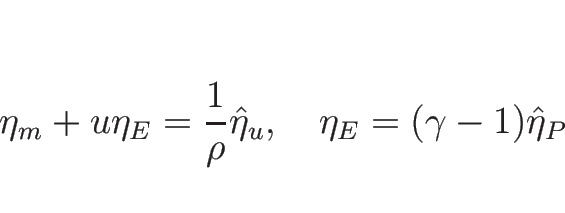
![\begin{displaymath}
B=\left[\begin{array}{ccc}
0 & \hat{\eta}_u/\rho & 0\\
\h...
...amma-1)\rho\hat{\eta}_P & 0 \\
0 & 0 & 0
\end{array}\right]
\end{displaymath}](img1447.png)
![]() に対して、
に対して、
![]() を求める。
(B.3) より、
を求める。
(B.3) より、
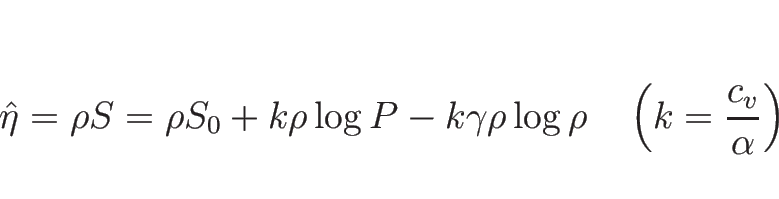
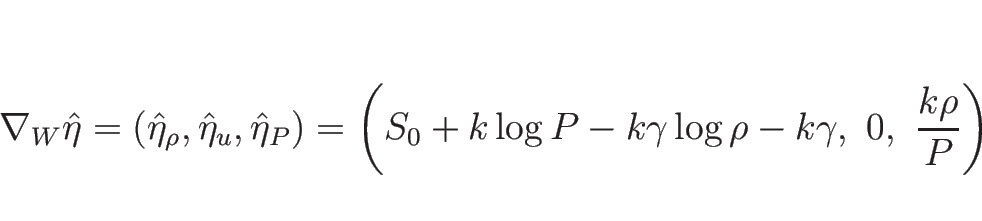
![\begin{displaymath}
\nabla_W^2\hat{\eta}=\left[\begin{array}{ccc}
-k\gamma/\rho...
... 0 & k(\gamma-1)\rho^2/P & 0\\
0 & 0 & 0
\end{array}\right]
\end{displaymath}](img1452.png)
![\begin{displaymath}
\nabla_W^2\hat{\eta}-B
=\left[\begin{array}{ccc}
-k\gamma/\...
...a-1)\rho^2/P & 0 \\
k/P & 0 & -k\rho/P^2
\end{array}\right]
\end{displaymath}](img1453.png)