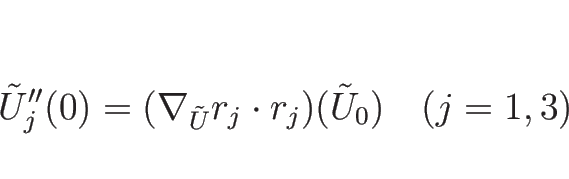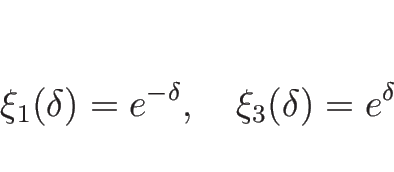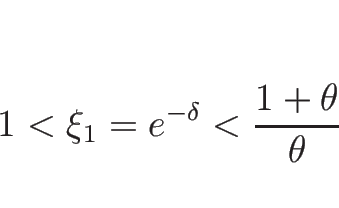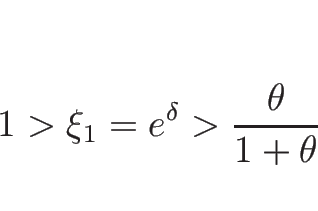4.9 ラグランジュ座標系の理想気体の場合
次はラグランジュ座標の方程式 (2.19) の場合を考える。
ランキン-ユゴニオ条件はこの場合、
![\begin{displaymath}
\begin{array}{l}
\tilde{s}[\tilde{v}]=[\tilde{u}],\\
\ti...
...frac{\tilde{u}^2}{2}+\frac{\tilde{P}\tilde{v}}{\gamma-1}\right)\end{displaymath}](img883.png) |
(4.104) |
となる。
2-接触不連続の場合、
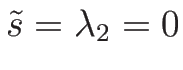 であるから、
(4.55) より
であるから、
(4.55) より
となる。これは、4.8 節の
オイラー座標系の場合に対応している。
(4.55) から 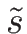 を消去すると、
を消去すると、
が得られるが、(4.57) の右辺は
4.8 節と同様に、
(4.57) の左辺も
4.8 節と同様にして
となるから、結局
となる。![$[\tilde{u}]=0$](img894.png) だとすると、1,3-衝撃波では
だとすると、1,3-衝撃波では
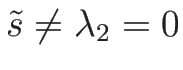 であるから、
(4.55) より
であるから、
(4.55) より
![$[\tilde{v}]=[\tilde{P}]=0$](img896.png) となってしまって
となってしまって ![$[\tilde{U}]=0$](img897.png) となるので
となるので
![$[\tilde{u}]\neq 0$](img898.png) であることがわかる。
よって、
であることがわかる。
よって、
となる。よって、展開して整理すると、
となるので、
とすると、
となり、これらも 4.8 節の結果に対応する。
また、(4.56) より、
なので、
となる。よって、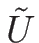 は
は
と書けることになる。これを
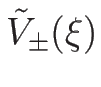 とすると、
とすると、
より、
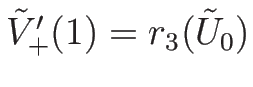 ,
,
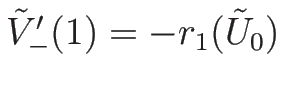 となり、
となり、
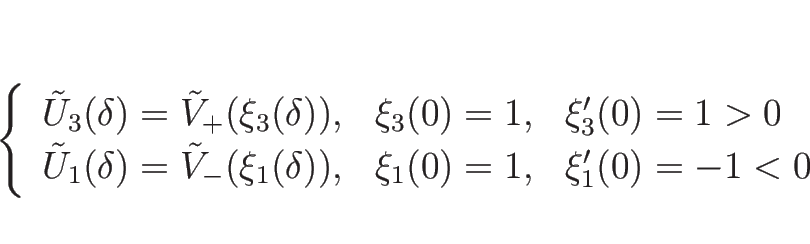 |
(4.107) |
によって、
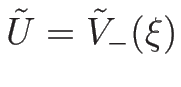 (
(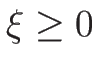 ) が 1-衝撃波曲線、
) が 1-衝撃波曲線、
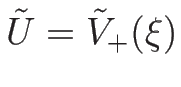 (
(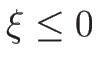 ) が 3-衝撃波曲線
となることがわかる。
) が 3-衝撃波曲線
となることがわかる。
衝撃波速度 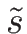 は、
は、
となる。(4.53), (3.23) より、
となる。
また、
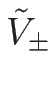 の 2 階微分は
の 2 階微分は
となるが、
となるので、
となる。
よって、(4.58) にさらに
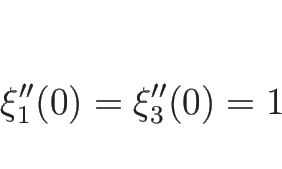 |
(4.108) |
であれば、
となる。
この (4.58), (4.59) を満たす 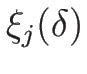 としては、
としては、
と取ればよい (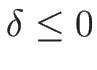 )。
この場合も、
)。
この場合も、
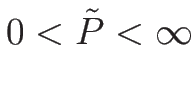 である必要があるので、
である必要があるので、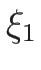 の方は
の方は
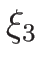 の方は
の方は
である必要がある。
竹野茂治@新潟工科大学
2018-08-01
![\begin{displaymath}
\begin{array}{l}
\tilde{s}[\tilde{v}]=[\tilde{u}],\\
\ti...
...frac{\tilde{u}^2}{2}+\frac{\tilde{P}\tilde{v}}{\gamma-1}\right)\end{displaymath}](img883.png)
![]() であるから、
(4.55) より
であるから、
(4.55) より
![\begin{displaymath}[\tilde{u}]=[\tilde{P}]=0
\end{displaymath}](img885.png)
![]() を消去すると、
を消去すると、
![\begin{eqnarray*}-[\tilde{u}][\tilde{B}]
&=&
-[\tilde{u}]\frac{1}{2}[\tilde{u}...
...}][\tilde{v}]
-\frac{1}{\gamma-1}[\tilde{u}][\tilde{P}\tilde{v}]\end{eqnarray*}](img891.png)
![\begin{displaymath}[\tilde{P}\tilde{u}][\tilde{v}]
=\frac{\tilde{u}_0+\tilde{u}}...
...lde{v}]
+\frac{\tilde{P}_0+\tilde{P}}{2}[\tilde{u}][\tilde{v}]
\end{displaymath}](img892.png)
![\begin{displaymath}
\frac{\tilde{P}_0+\tilde{P}}{2}[\tilde{u}][\tilde{v}]
=-\frac{1}{\gamma-1}[\tilde{u}][\tilde{P}\tilde{v}]
\end{displaymath}](img893.png)
![\begin{displaymath}
\frac{\tilde{P}_0+\tilde{P}}{2}[\tilde{v}]
=-\frac{1}{\gamma-1}[\tilde{P}\tilde{v}]
\end{displaymath}](img899.png)
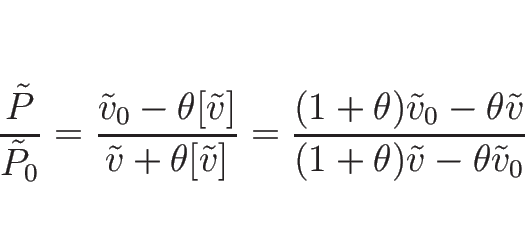
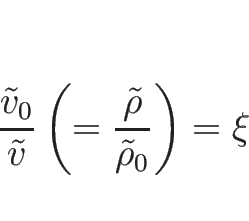
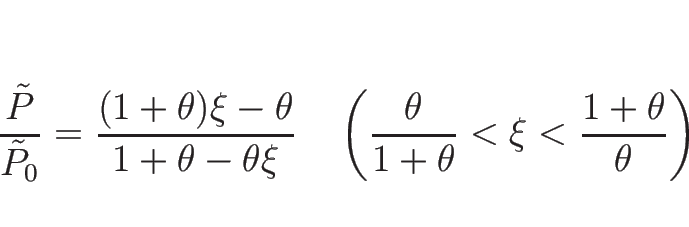
![\begin{eqnarray*}[\tilde{u}]^2
&=&
-[\tilde{P}[\tilde{v}]
=
-\left(\frac{\ti...
...hspace{1zw}\left(\tilde{C}=\sqrt{\gamma\tilde{P}\tilde{v}}\right)\end{eqnarray*}](img903.png)
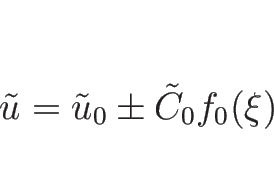
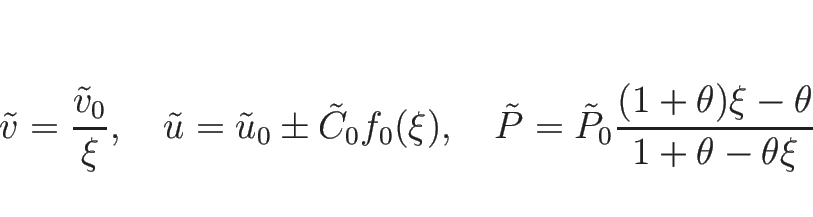
![\begin{displaymath}
\tilde{V}_{\pm}(1)=\left[\begin{array}{c}-\tilde{v}_0\\ \pm\tilde{C}_0\\ \gamma\tilde{P}_0\end{array}\right]
\end{displaymath}](img908.png)
![]() は、
は、
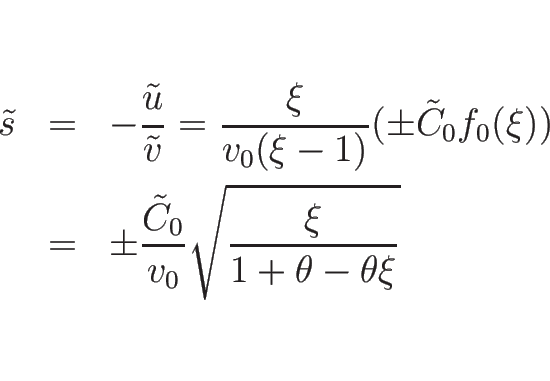
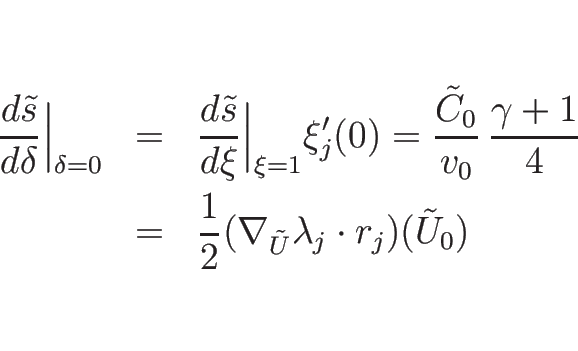
![]() の 2 階微分は
の 2 階微分は
![\begin{displaymath}
\tilde{V}_{\pm}''(1)
=\left[\begin{array}{c}2\tilde{v}_0\\ \...
...theta)\tilde{C}_0\\ 2\theta\gamma\tilde{P}_0\end{array}\right]
\end{displaymath}](img917.png)
![\begin{eqnarray*}\nabla_{\tilde{U}}r_1\cdot r_1
&=&
\nabla_{\tilde{U}}
\left[...
...\tilde{v}\\ \theta\tilde{C}\\ \gamma^2\tilde{P}\end{array}\right]\end{eqnarray*}](img918.png)
![\begin{eqnarray*}(\nabla_{\tilde{U}}r_1\cdot r_1)(\tilde{U}_0)+r_1(\tilde{U}_0)
...
...\ 2\theta\gamma\tilde{P}_0\end{array}\right]
=\tilde{V}_{+}''(1)\end{eqnarray*}](img919.png)