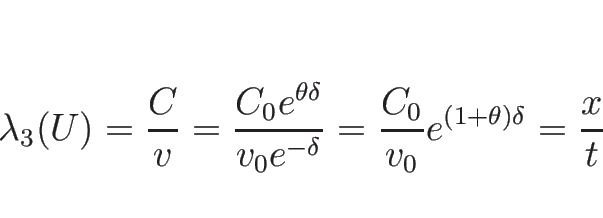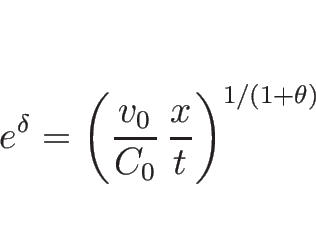3.6 ラグランジュ座標系の理想気体の場合の例
次に、2.6 節のラグランジュ座標系での方程式系
(2.19) に対して、同様の考察を行う。
ここでは、(2.19) は  は外して、
また
は外して、
また 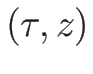 も
も 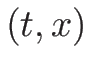 と書くことにする。
と書くことにする。
まず、(2.19) を
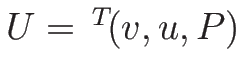 に関する
準線形の方程式系に書き直す。
に関する
準線形の方程式系に書き直す。
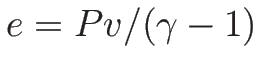 であるから、
最後のエネルギー保存の方程式は、
であるから、
最後のエネルギー保存の方程式は、
となるので、結局この場合は、
となる。
より、固有値は
固有ベクトルは
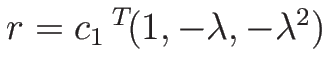 ととればよいので、
ととればよいので、
となる。
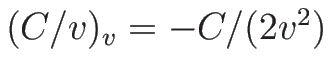 ,
,
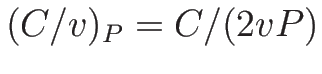 より、
より、
となり、2-特性方向は線形退化、
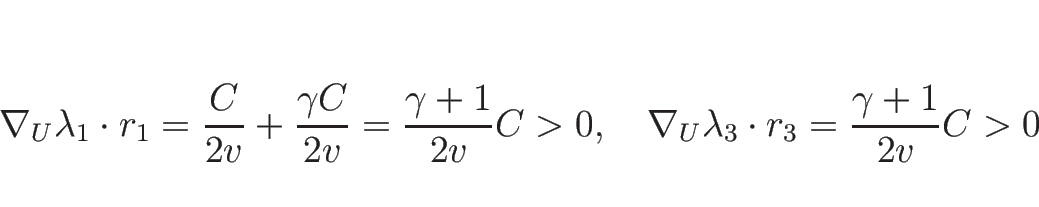 |
(3.42) |
なので、1-特性方向、3-特性方向は真性非線形となる。
リーマン不変量は、2-リーマン不変量は
より  ,
,  が 2-リーマン不変量で、1-リーマン不変量は、
が 2-リーマン不変量で、1-リーマン不変量は、
より、常微分方程式
を解くと、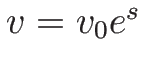 ,
,
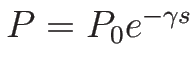 で、
で、
より
となるので、
より、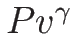 ,
, 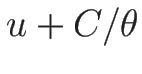 が 1-リーマン不変量、
同様にして 3-リーマン不変量は
が 1-リーマン不変量、
同様にして 3-リーマン不変量は 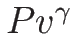 ,
, 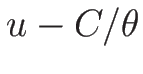 がそれであることがわかり、
よってリーマン不変量は、ラグランジュ座標とオイラー座標で
不変であることがわかる。
また、
がそれであることがわかり、
よってリーマン不変量は、ラグランジュ座標とオイラー座標で
不変であることがわかる。
また、
であるので、上の 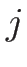 -リーマン不変量に
-リーマン不変量に 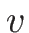 を追加すると、
それが相空間
を追加すると、
それが相空間 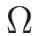 上で
上で 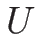 と 1 対 1 に対応する。
と 1 対 1 に対応する。
このパラメータに関しては、
なので、1-膨張波曲線 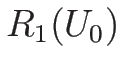 は
は 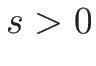 で得られ、よって、
で得られ、よって、
またはパラメータ表示により、
![\begin{displaymath}
\left\{\begin{array}{l}
v=v_0e^s,\\
\displaystyle u=u_0-...
...]
P=P_0e^{-\gamma s}
\end{array}\right. \hspace{1zw}(s\geq 0)\end{displaymath}](img427.png) |
(3.43) |
と表され、1-膨張波曲線 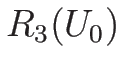 は、
は、
またはパラメータ表示により、
![\begin{displaymath}
\left\{\begin{array}{l}
v=v_0e^s,\\ [.5zh]
\displaystyle ...
...]
P=P_0e^{-\gamma s}
\end{array}\right. \hspace{1zw}(s\leq 0)\end{displaymath}](img429.png) |
(3.44) |
と表される。
この 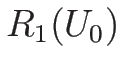 に対しては
に対しては  、
、
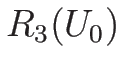 に対しては
に対しては 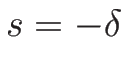 とすれば、いずれの場合も
とすれば、いずれの場合も
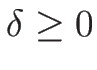 で、
で、
を満たす。
また、膨張波解を 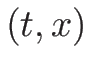 で表わすために、
(3.24) (
で表わすために、
(3.24) ( )
を
)
を
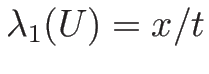 に代入すれば、
に代入すれば、
より、
となる。これを (3.24) ( ) に代入すれば 1-膨張波が
) に代入すれば 1-膨張波が 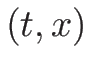 の式で表される。
この場合は、オイラー座標の場合とは異なり、
の式で表される。
この場合は、オイラー座標の場合とは異なり、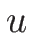 は
は 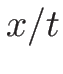 の一次式とはならない。
の一次式とはならない。
3-膨張波の方も、
(3.25) (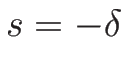 ) を
) を
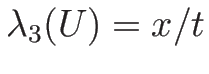 に代入すれば、
に代入すれば、
より、
となり、これを (3.25) (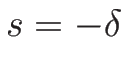 ) に代入すれば 3-膨張波が
) に代入すれば 3-膨張波が  の式で表される。
の式で表される。
竹野茂治@新潟工科大学
2018-08-01
![]() は外して、
また
は外して、
また ![]() も
も ![]() と書くことにする。
と書くことにする。
![]() に関する
準線形の方程式系に書き直す。
に関する
準線形の方程式系に書き直す。
![]() であるから、
最後のエネルギー保存の方程式は、
であるから、
最後のエネルギー保存の方程式は、
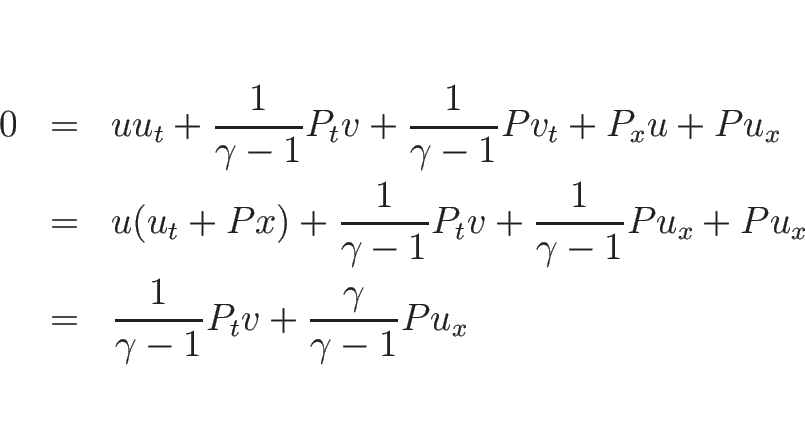
![\begin{displaymath}
\left[\begin{array}{c}v\\ u\\ P\end{array}\right]_t
+\left[\...
...right]
\left[\begin{array}{c}v \\ u\\ P\end{array}\right]_x
=0
\end{displaymath}](img403.png)
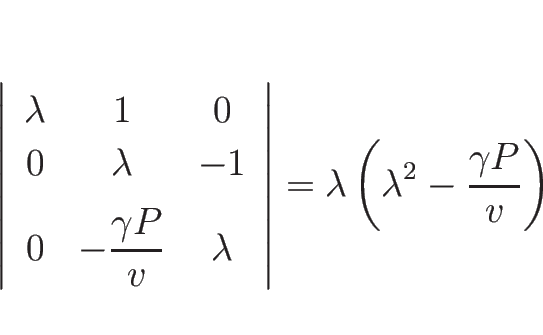
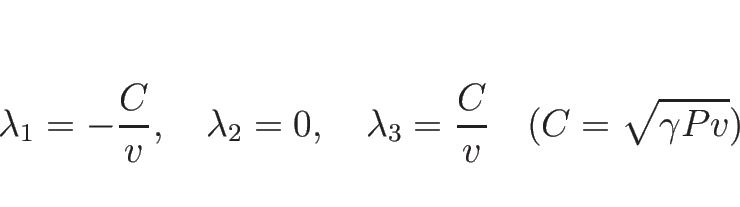
![\begin{displaymath}
r_1=\left[\begin{array}{c}v\\ C \\ -\gamma P\end{array}\righ...
...r_3=\left[\begin{array}{c}-v\\ C \\ \gamma P\end{array}\right]
\end{displaymath}](img407.png)
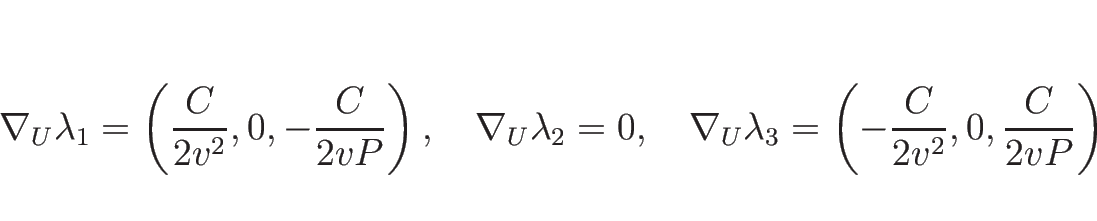
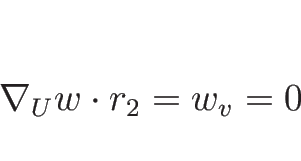
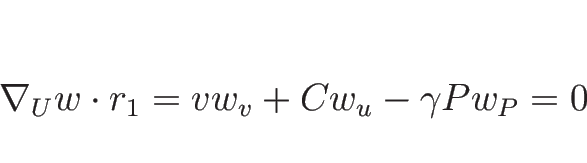
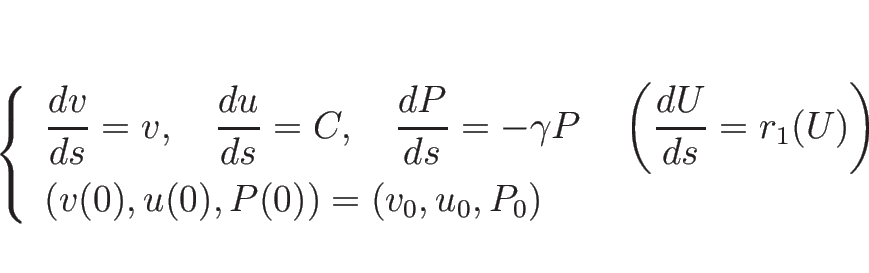
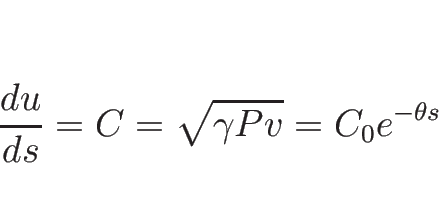
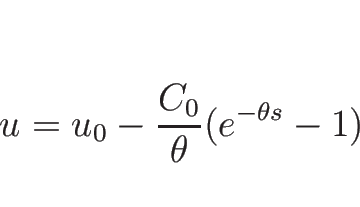
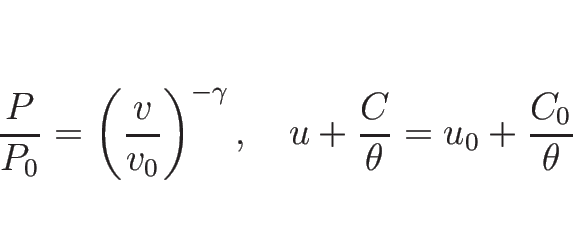
![\begin{displaymath}
\nabla_U v\cdot r_j=\left[\begin{array}{c}1\\ 0\\ 0\end{array}\right]r_j\neq 0
\hspace{1zw}(\mbox{$\pm v$\ または 1})
\end{displaymath}](img422.png)
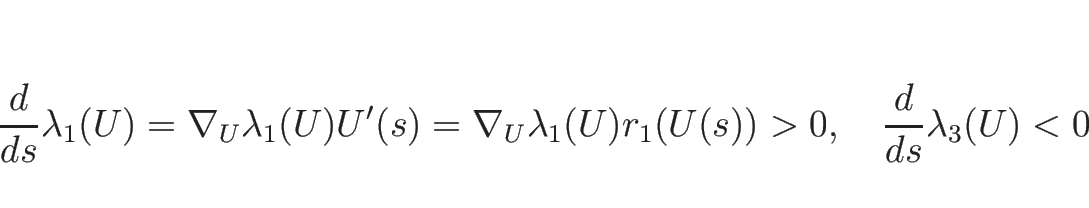
![\begin{displaymath}
\left\{\begin{array}{l}
Pv^\gamma=P_0v_0^\gamma,\\ [.5zh]
...
...e{1zw}(v\geq v_0,\hspace{1zw}, P\leq P_0,\hspace{1zw}u\geq u_0)\end{displaymath}](img426.png)
![\begin{displaymath}
\left\{\begin{array}{l}
Pv^\gamma=P_0v_0^\gamma,\\ [.5zh]
...
...e{1zw}(v\leq v_0,\hspace{1zw}, P\geq P_0,\hspace{1zw}u\geq u_0)\end{displaymath}](img428.png)
![]() に対しては
に対しては ![]() 、
、
![]() に対しては
に対しては ![]() とすれば、いずれの場合も
とすれば、いずれの場合も
![]() で、
で、
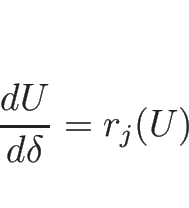
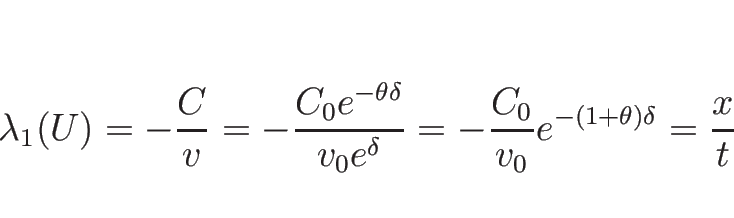
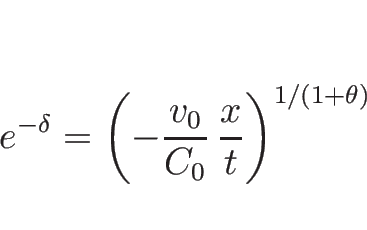
![]() ) を
) を
![]() に代入すれば、
に代入すれば、