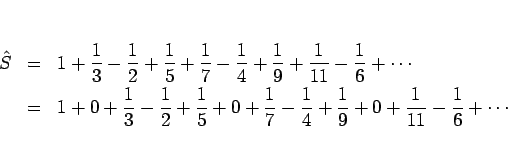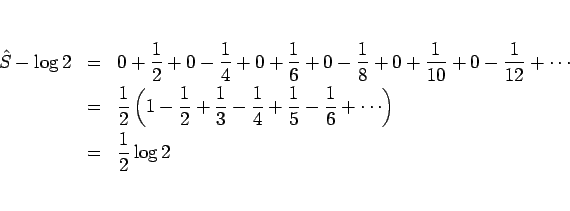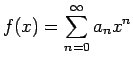 の収束半径が
の収束半径が 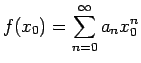 が収束するならば、
それは収束円内からの極限に一致する。すなわち、
が収束するならば、
それは収束円内からの極限に一致する。すなわち、
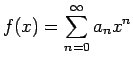 の収束半径が
の収束半径が ![]() (
(![]() )
であるとき、
)
であるとき、![]() となる
となる ![]() で
で
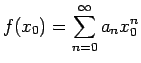 が収束するならば、
それは収束円内からの極限に一致する。すなわち、
が収束するならば、
それは収束円内からの極限に一致する。すなわち、
この証明は参考のために書き残しておくが、いわゆる ![]() -
-![]() 論法、
論法、
![]() , アーベル変形などを利用する煩雑なものなので、
読みとばしても構わない。
, アーベル変形などを利用する煩雑なものなので、
読みとばしても構わない。
証明
![]() ,
, ![]() をそれぞれ
をそれぞれ ![]() での和、部分和
での和、部分和
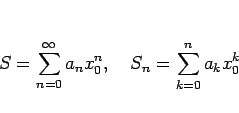
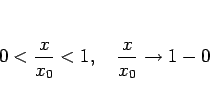
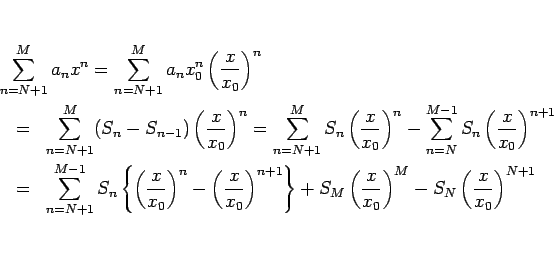
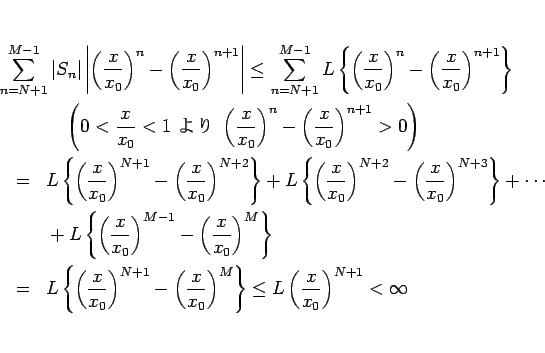
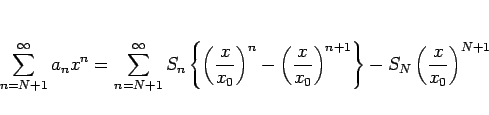
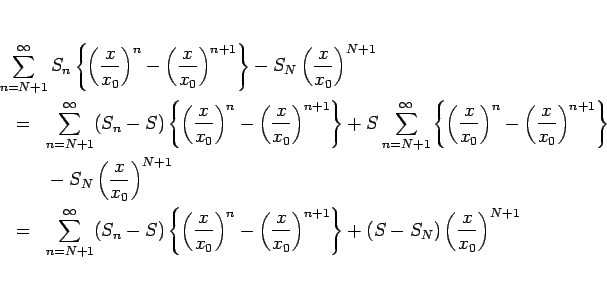
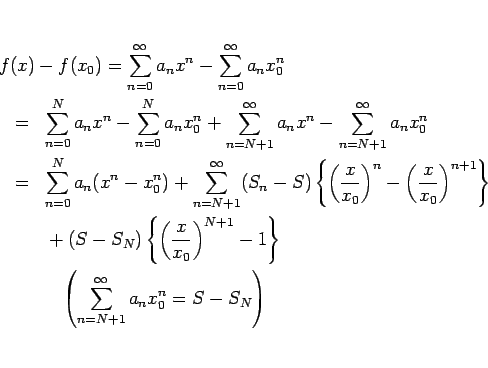
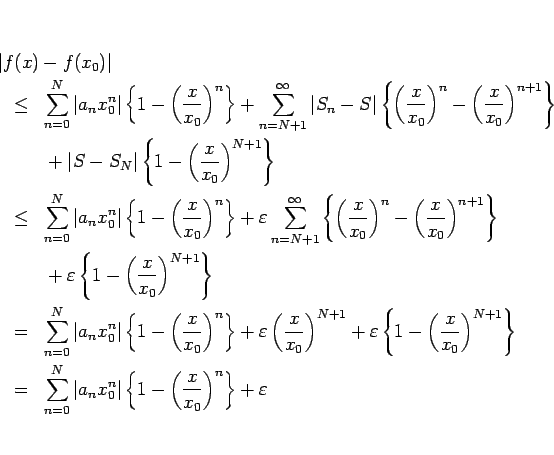
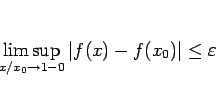
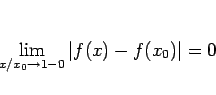
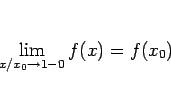
この定理 21 により、 収束円周上でその級数が収束する場合は内部からの極限に等しいことが言えるが、 しかし逆に収束円周上の収束性が保証されていない場合は、 内部から極限があったとしてもそれに一致するとは限らないことに注意する。
また収束円周上の値は、それが収束するギリギリのところであるから、 一般にその収束はかなり遅いので、あまり実用にはならない。
例えば収束する級数 (4) は、
![]() のマクローリン展開 (12) の
収束円周上
のマクローリン展開 (12) の
収束円周上 ![]() での値に等しく、よって定理 21 により
での値に等しく、よって定理 21 により
![]() であることが言えるが、
であることが言えるが、
![]() の計算をするならば (15) の式を用いる方が
ずっと精度はよい。
(4) を使用する場合は、命題 3 より
2 項ずつまとめたとしても、10 項目はだいたい
の計算をするならば (15) の式を用いる方が
ずっと精度はよい。
(4) を使用する場合は、命題 3 より
2 項ずつまとめたとしても、10 項目はだいたい
![]() くらいであるが、(15) の式の場合は、
10 項目はだいたい
くらいであるが、(15) の式の場合は、
10 項目はだいたい
![]() くらいになっている。
くらいになっている。
また、![]() のマクローリン展開 (14) を利用すれば、
これに
のマクローリン展開 (14) を利用すれば、
これに ![]() を代入することで、
を代入することで、
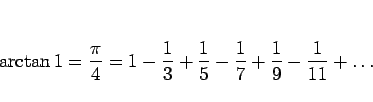
この節の最後に、(4) が ![]() に等しいことを
積分を使って直接示す方法、および、(5) が
に等しいことを
積分を使って直接示す方法、および、(5) が ![]() に等しいことを示す。そのために、よく知られている以下の公式
(区分求積) を利用する。
に等しいことを示す。そのために、よく知られている以下の公式
(区分求積) を利用する。
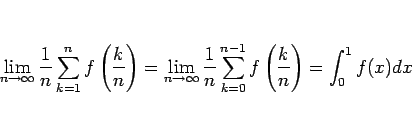
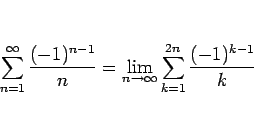
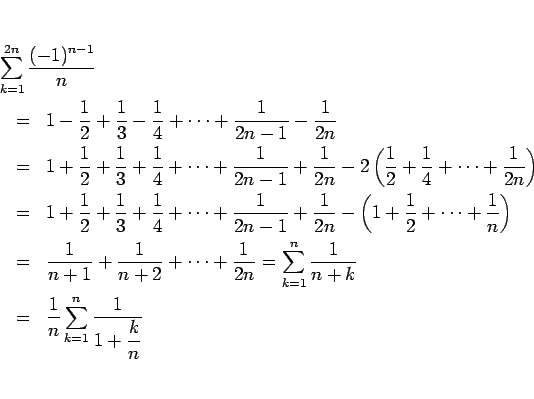
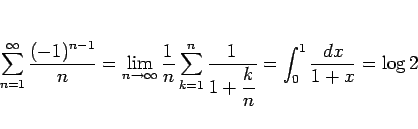
(5) の方は以下のようにすればよい。まず、 2,6,10,...項目に 0 をはさんで