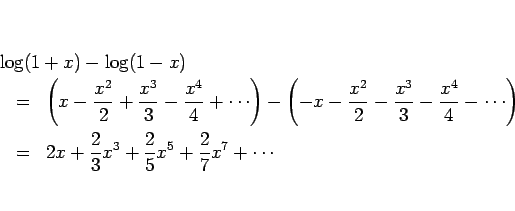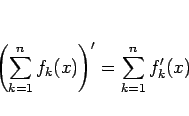
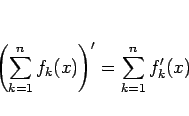
しかし、ベキ級数の項別微分可能性に関しては、次の定理がなりたつ。
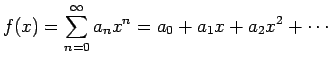 の収束半径を
の収束半径を ![]() とすると、
形式的に項別に微分して得られるベキ級数
とすると、
形式的に項別に微分して得られるベキ級数
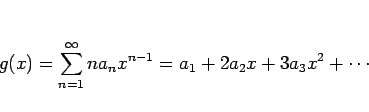
証明
一般の場合の証明は面倒なので、簡単のため、
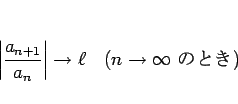
まず、
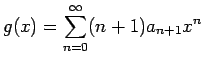 の収束半径も
の収束半径も ![]() であることは、
であることは、
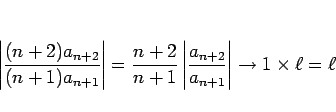
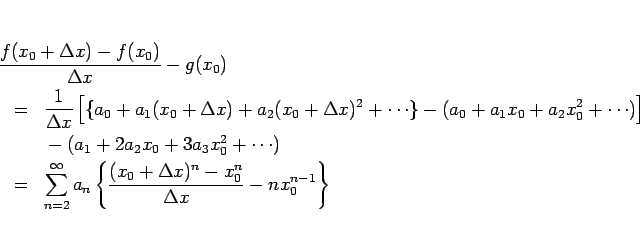
「が
で 2 回微分可能で、
がそこで連続ならば、
に対して
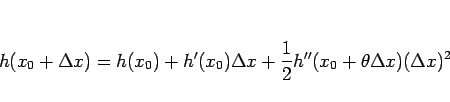
となるこれにより、すべての(
) が存在する (
は
にも依存する)。」
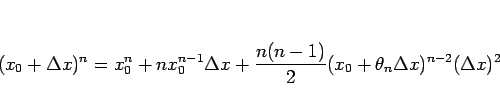
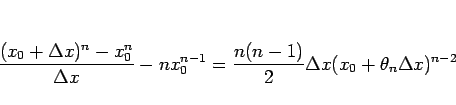
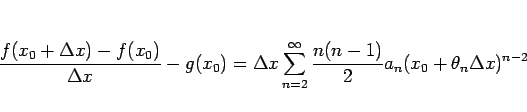
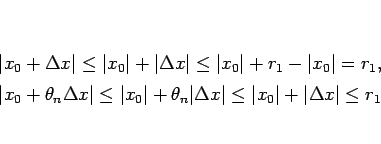
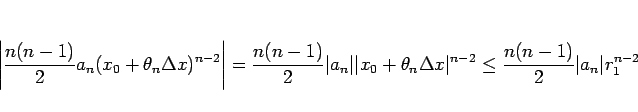
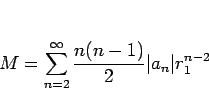
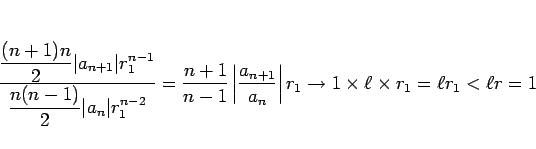
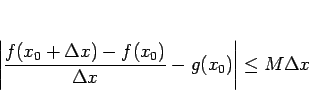
この定理 12 により、
ベキ級数は収束半径内で何回でも微分可能であることになる
(こういう関数を 無限回微分可能、![]() 級、
あるいは なめらかな関数 と呼ぶことがある) であることがわかる。
逆に、そうでない関数はベキ級数展開できない。
これはフーリエ級数が不連続な関数でも展開できるのとは大いに異なる点である。
級、
あるいは なめらかな関数 と呼ぶことがある) であることがわかる。
逆に、そうでない関数はベキ級数展開できない。
これはフーリエ級数が不連続な関数でも展開できるのとは大いに異なる点である。
また、「ベキ級数展開できる」という性質は無限回微分可能という性質よりも強い ことになるが、よってベキ級数展開できる関数のことを 解析的 と呼んで、 無限回微分可能と区別することがある。
この定理 12 により、 ベキ級数は自由に項別微分ができることになるが、 実際にいくつか計算してみる。
![]() のマクローリン展開
のマクローリン展開
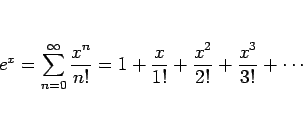
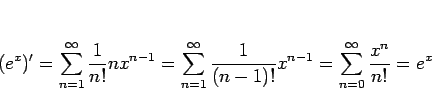
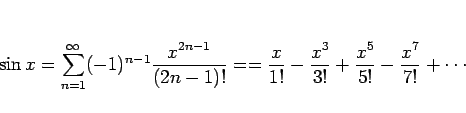
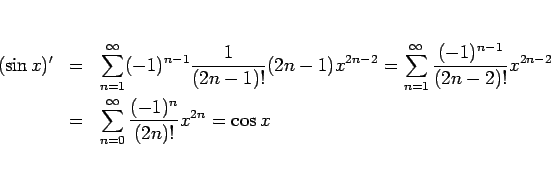
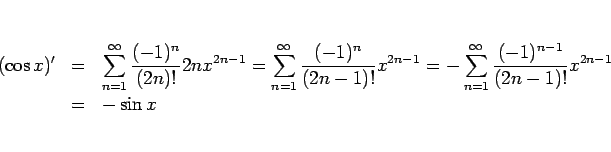
無限等比級数の公式
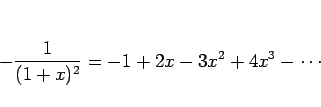
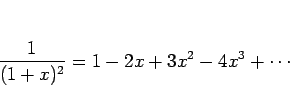
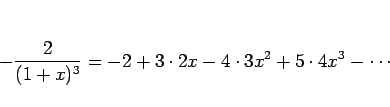
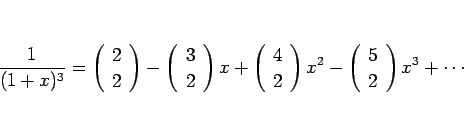
微分の逆を考えれば、次の項別積分の定理が得られる。
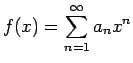 の収束半径が
の収束半径が ![]() であるとき、
であるとき、
![]() の原始関数
の原始関数 ![]() (
(![]() ) は、
) は、
これは、(11) で与えられるベキ級数を ![]() とおいて、
これに定理 12 を適用すれば、
とおいて、
これに定理 12 を適用すれば、
![]() であって収束半径が
であって収束半径が ![]() であることがわかり、
であることがわかり、
![]() なので、
なので、![]() であることが言える。
であることが言える。
これを使うと例えば、(10) から、これを積分して
また、(12) の式からは ![]() の値を
求めることはできないが (
の値を
求めることはできないが (![]() は収束半径の内側ではないので代入できない)、
(12) の
は収束半径の内側ではないので代入できない)、
(12) の ![]() の代わりに
の代わりに ![]() を代入して、
(12) から引き算すると、
を代入して、
(12) から引き算すると、