4 オイラー方程式の解
本節では、3 節で得られたオイラー方程式を
満たす関数を求める。
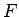 が陽に
が陽に 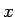 に依存しない場合、
オイラー方程式 (16) は
容易に 1 回積分できることが知られている。
まず、それを紹介する。
に依存しない場合、
オイラー方程式 (16) は
容易に 1 回積分できることが知られている。
まず、それを紹介する。
(16) は、
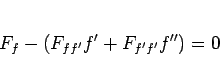 |
(17) |
という 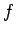 の 2 階の微分方程式に変形できるが、
の 2 階の微分方程式に変形できるが、
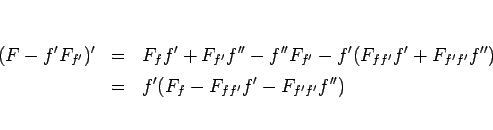
なので、(17) より
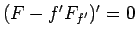 となり、よって
となり、よって
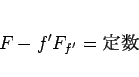 |
(18) |
となる。これは、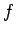 の 1 階の微分方程式となる。
の 1 階の微分方程式となる。
さて、最速降下線の問題の場合、
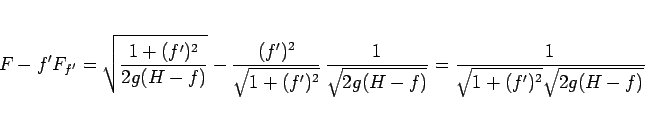
となるので、
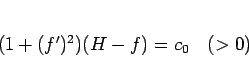 |
(19) |
となり、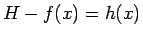 とすると、
とすると、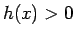 (
(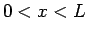 ),
), 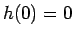 ,
, 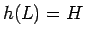 で、
で、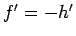 より、
より、
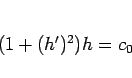 |
(20) |
となる。これは、変数分離形の微分方程式であり、
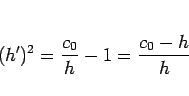
より、
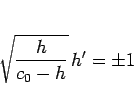 |
(21) |
となり、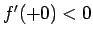 より
より 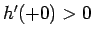 であるから、
少なくとも
であるから、
少なくとも 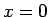 の付近では、符号は正で、
これを
の付近では、符号は正で、
これを 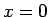 から
から 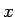 まで積分すれば、
まで積分すれば、
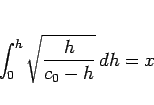 |
(22) |
が得られる。
(20) より、
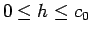 でなければいけないことになるが、
(22) で
でなければいけないことになるが、
(22) で 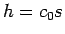 とすると、
とすると、
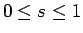 で、
で、
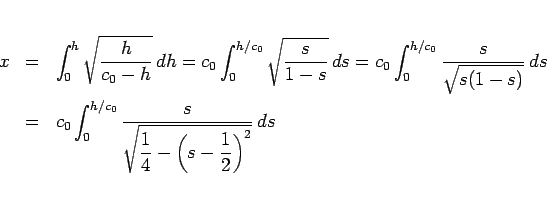
となる。よって、
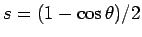
 と置換すると、
と置換すると、
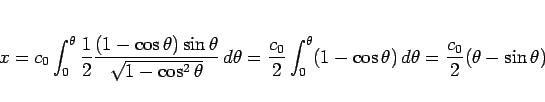
となる。ここで、この 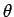 は
は
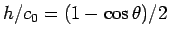 を満たすものなので、
結局
を満たすものなので、
結局 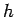 と
と 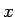 は、
は、
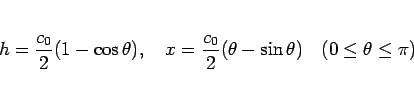 |
(23) |
によって結びつくことになる。
これは、良く知られているように「サイクロイド曲線」を
全体的に拡大 (または縮小) したグラフの
パラメータ表示になっていて、
直径 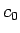 の車輪で作られるサイクロイドになる。
の車輪で作られるサイクロイドになる。
よって、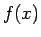 は、これを上下逆にした「逆さサイクロイド」
として
は、これを上下逆にした「逆さサイクロイド」
として 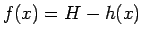 によって作られることになる。
次節で、この「サイクロイド曲線」について詳しく見ることにする。
によって作られることになる。
次節で、この「サイクロイド曲線」について詳しく見ることにする。
竹野茂治@新潟工科大学
2016年1月8日
![]() が陽に
が陽に ![]() に依存しない場合、
オイラー方程式 (16) は
容易に 1 回積分できることが知られている。
まず、それを紹介する。
に依存しない場合、
オイラー方程式 (16) は
容易に 1 回積分できることが知られている。
まず、それを紹介する。
![]() でなければいけないことになるが、
(22) で
でなければいけないことになるが、
(22) で ![]() とすると、
とすると、
![]() で、
で、
![]() は、これを上下逆にした「逆さサイクロイド」
として
は、これを上下逆にした「逆さサイクロイド」
として ![]() によって作られることになる。
次節で、この「サイクロイド曲線」について詳しく見ることにする。
によって作られることになる。
次節で、この「サイクロイド曲線」について詳しく見ることにする。