9 最速であることの証明
変分法は、汎関数の最小を与える関数の候補を導くだけで、
実際にそれが本当に最小を与えているのかについては、
別の考察が必要となる。
汎関数の凸性を利用する方法などもあるようだが、
本節では、実際に逆さサイクロイドが最小値を与えることの
証明を紹介する。
本来、変分問題の最小性の証明は易しくはないが、
最速降下線問題については、初等的な証明も知られている。
[2], [11] でも紹介されている [6] の証明は
シュワルツの不等式を利用した非常にシンプルなものであるが、
これは A と B が水平な位置にある場合、
すなわち
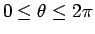 の逆さサイクロイド全体が解になる
場合にしか適用できない。
の逆さサイクロイド全体が解になる
場合にしか適用できない。
一方、[7] はわずか 2 ページの論文だが、
その証明は A, B の一般の位置に対するもので、
シュワルツの不等式に少し追加した不等式を用いることで、
初等的で非常に鮮やかな証明を行っている。
本節では、[7] に習い、
しかしその証明の流れを少し変えた証明を紹介する。
目標は、
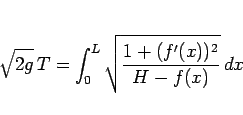 |
(52) |
を最小化する関数 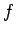 が逆さサイクロイドであることを示すことである。
が逆さサイクロイドであることを示すことである。
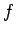 は、
は、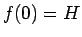 ,
, 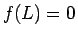 で、
で、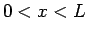 では
では 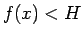 を満たす、
滑らかな関数とする。
を満たす、
滑らかな関数とする。
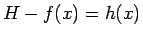 と書けば、(52) は、
と書けば、(52) は、
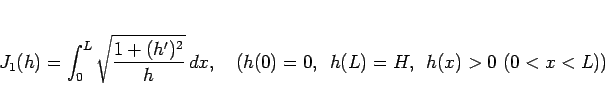 |
(53) |
と書くことができ、そしてこれを最小化するのがサイクロイド関数
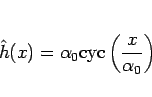
であることを示す。
ここで 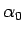 は、7 節で見たように、
は、7 節で見たように、
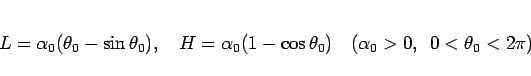
によって 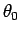 とともに一意に決まるものである。
とともに一意に決まるものである。
シュワルツの不等式
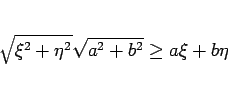 |
(54) |
は、良く知られているように
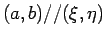 のときに等号が成立する。
これを用いると、
のときに等号が成立する。
これを用いると、
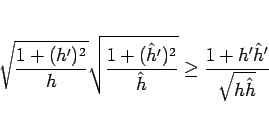 |
(55) |
となる。これをさらに、以下のように変形する。
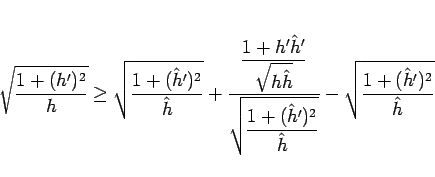 |
(56) |
そして、右辺の後の方の 2 項の和を 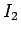 とする。
とする。
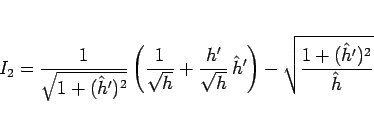 |
(57) |
ここからの証明の方針は以下の通り。
(56) より、
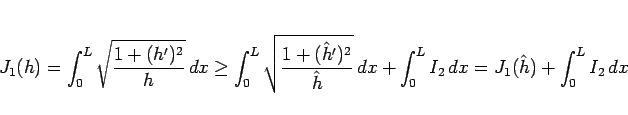
となるが、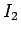 は
は
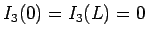 ,
, 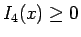 と
なる
と
なる 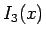 ,
, 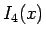 により、
により、
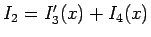 の形に分けることができて、よって、
の形に分けることができて、よって、
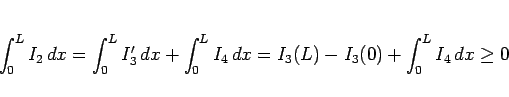
となり、よって
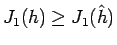 が成り立つことになるので、
が成り立つことになるので、
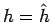 のときに
のときに 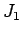 が最小となることが示される。
さらに、その等号成立の条件を検討すると、
が最小となることが示される。
さらに、その等号成立の条件を検討すると、
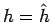 以外にはその最小を与える関数がないことも示される。
以外にはその最小を与える関数がないことも示される。
以下では 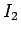 を上の形に分けることを考える。
まず、
を上の形に分けることを考える。
まず、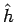 をパラメータ
をパラメータ 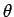 で表せば、
で表せば、
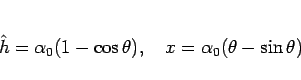
で、5 節で計算したように、
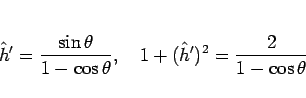
となり、よって、
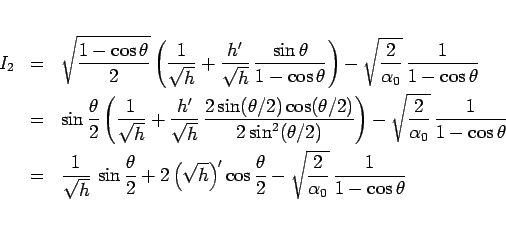
となる。
よって、 を作るために、
を作るために、
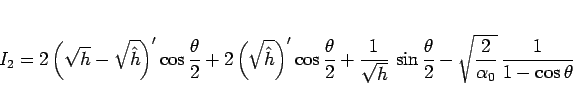
と変形すると、
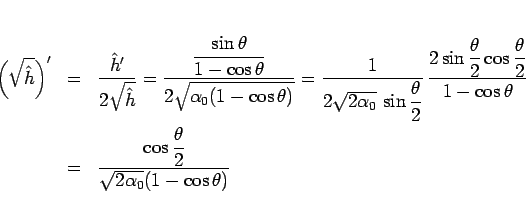
より、
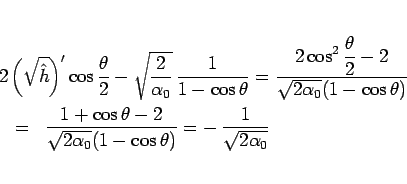
となるので、
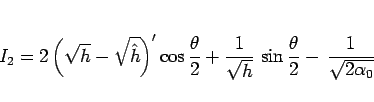
となる。よって、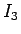 を
を
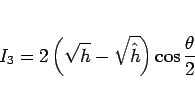 |
(58) |
とすると、
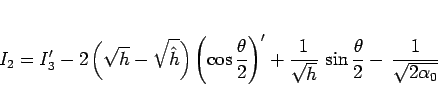
となるが、
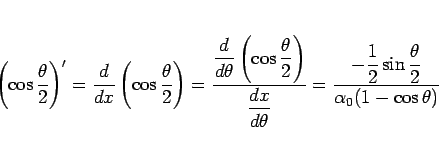
なので、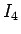 は、
は、
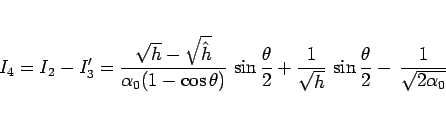
とすることになる。ここで
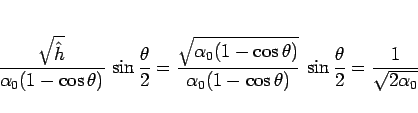
より、結局 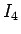 は
は
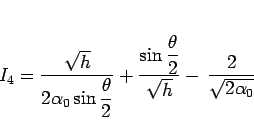
と書ける。この最初の 2 項に相乗・相加平均の不等式を用いると、
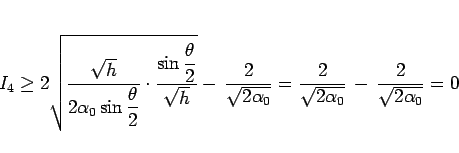 |
(59) |
が得られる。
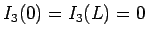 も、
(58) の形と
も、
(58) の形と 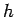 が
満たすべき境界条件により成り立つので、
これで上の方針通り、
が
満たすべき境界条件により成り立つので、
これで上の方針通り、
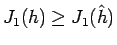 が示されたことになり、
サイクロイドが最小値を与えることが示された。
が示されたことになり、
サイクロイドが最小値を与えることが示された。
次に、この等号成立の条件であるが、
それはシュワルツの不等式 (55) と、
相乗・相加平均の不等式 (59) の両方の等号が
積分範囲のすべての 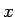 、すなわち
、すなわち 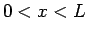 で成り立つこと、となるが、
シュワルツの不等式の方の等号は、
で成り立つこと、となるが、
シュワルツの不等式の方の等号は、
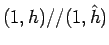 を意味するので、
これは
を意味するので、
これは 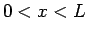 で
で 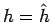 でなければいけないことを意味する。
つまり、こちらの条件だけで
でなければいけないことを意味する。
つまり、こちらの条件だけで
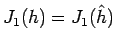 となる
となる 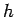 が
が 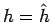 以外にないことがわかる。
以外にないことがわかる。
ちなみに、相乗・相加平均の不等式
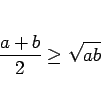
の等号成立条件は 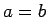 なので、こちらは、
なので、こちらは、
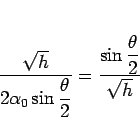
となるが、これは、
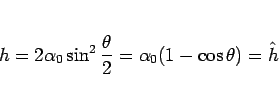
となり、こちらも実は 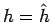 のときにのみ
等号が成立することがわかる。
のときにのみ
等号が成立することがわかる。
竹野茂治@新潟工科大学
2016年1月8日
![]() の逆さサイクロイド全体が解になる
場合にしか適用できない。
の逆さサイクロイド全体が解になる
場合にしか適用できない。
![]() と書けば、(52) は、
と書けば、(52) は、
![]() を上の形に分けることを考える。
まず、
を上の形に分けることを考える。
まず、![]() をパラメータ
をパラメータ ![]() で表せば、
で表せば、
![]() 、すなわち
、すなわち ![]() で成り立つこと、となるが、
シュワルツの不等式の方の等号は、
で成り立つこと、となるが、
シュワルツの不等式の方の等号は、
![]() を意味するので、
これは
を意味するので、
これは ![]() で
で ![]() でなければいけないことを意味する。
つまり、こちらの条件だけで
でなければいけないことを意味する。
つまり、こちらの条件だけで
![]() となる
となる ![]() が
が ![]() 以外にないことがわかる。
以外にないことがわかる。