2 漸近展開とは
[1] によれば、漸近展開の定義は以下のようになる。
定義 1
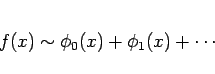 |
(1) |
(右辺は有限和、あるいは無限和) が、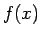 の 漸近展開 であるとは、
各
の 漸近展開 であるとは、
各  に対し、
に対し、
 に関して
次の 2 つが成り立つことである。
に関して
次の 2 つが成り立つことである。
-
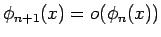 , すなわち、
, すなわち、
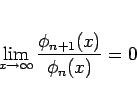 |
(2) |
-
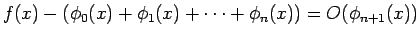 , すなわち、
, すなわち、
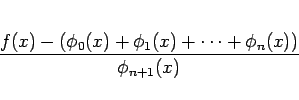
が
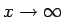 に関して有界
に関して有界
この (2) の 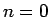 の場合は
の場合は
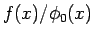 が
有界であることを意味するが、
が
有界であることを意味するが、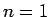 の場合を考えると、
の場合を考えると、
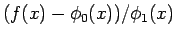 は有界で、
は有界で、
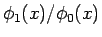 は 0 に収束するので、
は 0 に収束するので、
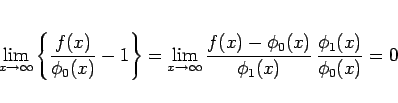
となり、結局
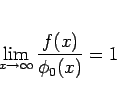 |
(3) |
となる。同様に、(1) の右辺が少なくとも 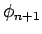 まで
続いていれば、
まで
続いていれば、
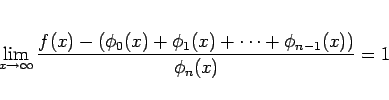
が成り立つ。
つまり、
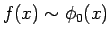 は (3) の意味で
は (3) の意味で
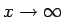 における第 1 近似、
における第 1 近似、
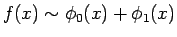 は、
は、
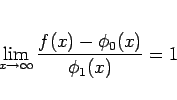
の意味で
 における第 2 近似、
といったものを表していることになる。
における第 2 近似、
といったものを表していることになる。
しかし、特に  が
が
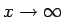 のときに
無限大に発散してしまう場合は、
テイラー展開などとは異なり、
誤差、すなわち左辺と右辺の差が
のときに
無限大に発散してしまう場合は、
テイラー展開などとは異なり、
誤差、すなわち左辺と右辺の差が
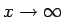 のときに小さくなる、
というわけではないことに注意する必要がある。
のときに小さくなる、
というわけではないことに注意する必要がある。
例えば、
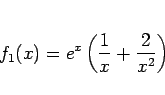
の場合、第 1 近似は
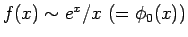 であるが、
これは、
であるが、
これは、
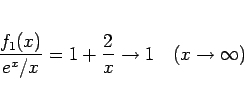
を意味するのであって、
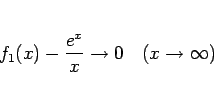
を意味するのではない。実際、この場合は、
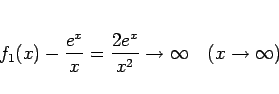
となっているから差は小さくはない。
また、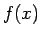 が
が
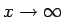 のときに有限であっても、
テイラー展開のように、
のときに有限であっても、
テイラー展開のように、
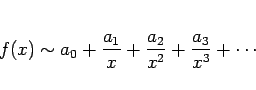
のようになる、すなわち 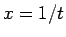 として
として 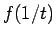 の
の 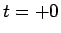 での
テイラー展開を考えればよい、というわけでもないことに注意する。
例えば、
での
テイラー展開を考えればよい、というわけでもないことに注意する。
例えば、
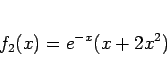
の場合、
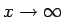 のときに
のときに
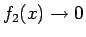 であるが、
であるが、
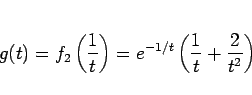
とすると、容易にわかるように  の
の  階微分は、
ある
階微分は、
ある  次の多項式
次の多項式 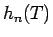 を用いて、
を用いて、
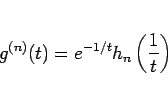
と書けるから、
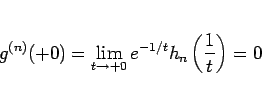
となり、よって 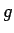 の
の 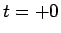 でのテイラー展開のすべての係数は 0 になってしまう。
でのテイラー展開のすべての係数は 0 になってしまう。
また、漸近展開は一意的でないことにも注意する。
例えば上の 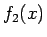 の場合、定義からすれば第 1 近似 (
の場合、定義からすれば第 1 近似 (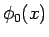 ) は
) は
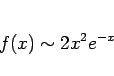
でも
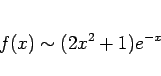
でも構わない。もちろん、より単純な式の方を取るのが普通である。
さらに、漸近展開 (1) の右辺が無限和である場合、
それは収束する級数であるとは限らないことに注意する。
これは、3 節の最後に例を紹介する。
竹野茂治@新潟工科大学
2010年4月8日
![]() の場合は
の場合は
![]() が
有界であることを意味するが、
が
有界であることを意味するが、![]() の場合を考えると、
の場合を考えると、
![]() は有界で、
は有界で、
![]() は 0 に収束するので、
は 0 に収束するので、
![]() は (3) の意味で
は (3) の意味で
![]() における第 1 近似、
における第 1 近似、
![]() は、
は、
![]() が
が
![]() のときに
無限大に発散してしまう場合は、
テイラー展開などとは異なり、
誤差、すなわち左辺と右辺の差が
のときに
無限大に発散してしまう場合は、
テイラー展開などとは異なり、
誤差、すなわち左辺と右辺の差が
![]() のときに小さくなる、
というわけではないことに注意する必要がある。
のときに小さくなる、
というわけではないことに注意する必要がある。
![]() が
が
![]() のときに有限であっても、
テイラー展開のように、
のときに有限であっても、
テイラー展開のように、
![]() の場合、定義からすれば第 1 近似 (
の場合、定義からすれば第 1 近似 (![]() ) は
) は