次へ: 6 公転による変化 上へ: 春分について 前へ: 4 観測点での座標系 (PDF ファイル: astro1.pdf)


5 太陽の軌道

P の地表平面に立つ観測者はこの $ \bar{{e}}_{x}^{}$ , $ \bar{{e}}_{y}^{}$ , $ \bar{{e}}_{z}^{}$ を 基本ベクトルとする座標系で観測するから、 P から太陽への位置ベクトル $ \overrightarrow{\mbox{\rm PO}}$ を この $ \bar{{e}}_{x}^{}$ , $ \bar{{e}}_{y}^{}$ , $ \bar{{e}}_{z}^{}$ で 表すことで太陽の見た目の軌道が得られる。

$ \overrightarrow{\mbox{\rm QP}}$ = r$ \bar{{e}}_{z}^{}$ であり、よって、

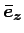
$\displaystyle \overrightarrow{\mbox{\rm PO}}$ = - $\displaystyle \overrightarrow{\mbox{\rm OP}}$ = - $\displaystyle \overrightarrow{\mbox{\rm OQ}}$ - r$\displaystyle \mbox{\boldmath$\bar{e}_z$}$ (5)
であるから、この $ \overrightarrow{\mbox{\rm OQ}}$ を $ \bar{{e}}_{x}^{}$ , $ \bar{{e}}_{y}^{}$ , $ \bar{{e}}_{z}^{}$ で表せばよい。 実際には、それぞれの方向への成分を求めればよいが、 それはそれぞれのベクトルとの内積で計算できる。

$ \overrightarrow{\mbox{\rm OQ}}$ = $ \rho$(cos$ \beta$, sin$ \beta$, 0) であるから、

$\displaystyle \overrightarrow{\mbox{\rm OQ}}$ . $\displaystyle \mbox{\boldmath$\omega$}$ = $\displaystyle \rho$(cos$\displaystyle \beta$, sin$\displaystyle \beta$, 0) . (0, sin$\displaystyle \alpha$, cos$\displaystyle \alpha$) = $\displaystyle \rho$sin$\displaystyle \alpha$sin$\displaystyle \beta$,  
$\displaystyle \overrightarrow{\mbox{\rm OQ}}$ . $\displaystyle \mbox{\boldmath$e_x$}$ = $\displaystyle \rho$(cos$\displaystyle \beta$, sin$\displaystyle \beta$, 0) . (1, 0, 0) = $\displaystyle \rho$cos$\displaystyle \beta$,  
$\displaystyle \overrightarrow{\mbox{\rm OQ}}$ . $\displaystyle \mbox{\boldmath$\tau$}$ = $\displaystyle \rho$(cos$\displaystyle \beta$, sin$\displaystyle \beta$, 0) . (0, cos$\displaystyle \alpha$, - sin$\displaystyle \alpha$) = $\displaystyle \rho$cos$\displaystyle \alpha$sin$\displaystyle \beta$  

となるので、よって、
$\displaystyle \overrightarrow{\mbox{\rm OQ}}$ . $\displaystyle \mbox{\boldmath$\bar{e}_x$}$ = - $\displaystyle \overrightarrow{\mbox{\rm OQ}}$ . $\displaystyle \mbox{\boldmath$e_x$}$sin t + $\displaystyle \overrightarrow{\mbox{\rm OQ}}$ . $\displaystyle \mbox{\boldmath$\tau$}$cos t  
  = $\displaystyle \rho$(- cos$\displaystyle \beta$sin t + cos$\displaystyle \alpha$sin$\displaystyle \beta$cos t),  
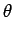
$\displaystyle \overrightarrow{\mbox{\rm OQ}}$ . $\displaystyle \mbox{\boldmath$\bar{e}_y$}$ = $\displaystyle \overrightarrow{\mbox{\rm OQ}}$ . $\displaystyle \mbox{\boldmath$\omega$}$cos$\displaystyle \theta$ - $\displaystyle \overrightarrow{\mbox{\rm OQ}}$ . $\displaystyle \mbox{\boldmath$e_x$}$sin$\displaystyle \theta$cos t - $\displaystyle \overrightarrow{\mbox{\rm OQ}}$ . $\displaystyle \mbox{\boldmath$\tau$}$sin$\displaystyle \theta$sin t  
  = $\displaystyle \rho$(sin$\displaystyle \alpha$sin$\displaystyle \beta$cos$\displaystyle \theta$ - cos$\displaystyle \beta$sin$\displaystyle \theta$cos t - cos$\displaystyle \alpha$sin$\displaystyle \beta$sin$\displaystyle \theta$sin t),  
$\displaystyle \overrightarrow{\mbox{\rm OQ}}$ . $\displaystyle \mbox{\boldmath$\bar{e}_z$}$ = $\displaystyle \overrightarrow{\mbox{\rm OQ}}$ . $\displaystyle \mbox{\boldmath$\omega$}$sin$\displaystyle \theta$ + $\displaystyle \overrightarrow{\mbox{\rm OQ}}$ . $\displaystyle \mbox{\boldmath$e_x$}$cos$\displaystyle \theta$cos t + $\displaystyle \overrightarrow{\mbox{\rm OQ}}$ . $\displaystyle \mbox{\boldmath$\tau$}$cos$\displaystyle \theta$sin t  
  = $\displaystyle \rho$(sin$\displaystyle \alpha$sin$\displaystyle \beta$sin$\displaystyle \theta$ + cos$\displaystyle \beta$cos$\displaystyle \theta$cos t + cos$\displaystyle \alpha$sin$\displaystyle \beta$cos$\displaystyle \theta$sin t)  

となる。よって、
$\displaystyle \overrightarrow{\mbox{\rm OQ}}$ = ($\displaystyle \overrightarrow{\mbox{\rm OQ}}$ . $\displaystyle \mbox{\boldmath$\bar{e}_x$}$)$\displaystyle \mbox{\boldmath$\bar{e}_x$}$ + ($\displaystyle \overrightarrow{\mbox{\rm OQ}}$ . $\displaystyle \mbox{\boldmath$\bar{e}_y$}$)$\displaystyle \mbox{\boldmath$\bar{e}_y$}$ + ($\displaystyle \overrightarrow{\mbox{\rm OQ}}$ . $\displaystyle \mbox{\boldmath$\bar{e}_z$}$)$\displaystyle \mbox{\boldmath$\bar{e}_z$}$  
  = $\displaystyle \rho$(- cos$\displaystyle \beta$sin t + cos$\displaystyle \alpha$sin$\displaystyle \beta$cos t)$\displaystyle \mbox{\boldmath$\bar{e}_x$}$  
    + $\displaystyle \rho$(sin$\displaystyle \alpha$sin$\displaystyle \beta$cos$\displaystyle \theta$ - cos$\displaystyle \beta$sin$\displaystyle \theta$cos t - cos$\displaystyle \alpha$sin$\displaystyle \beta$sin$\displaystyle \theta$sin t)$\displaystyle \mbox{\boldmath$\bar{e}_y$}$  
    + $\displaystyle \rho$(sin$\displaystyle \alpha$sin$\displaystyle \beta$sin$\displaystyle \theta$ + cos$\displaystyle \beta$cos$\displaystyle \theta$cos t + cos$\displaystyle \alpha$sin$\displaystyle \beta$cos$\displaystyle \theta$sin t)$\displaystyle \mbox{\boldmath$\bar{e}_z$}$  
  = $\displaystyle \rho$cos t($\displaystyle \mbox{\boldmath$\bar{e}_x$}$cos$\displaystyle \alpha$sin$\displaystyle \beta$ - $\displaystyle \mbox{\boldmath$\bar{e}_y$}$cos$\displaystyle \beta$sin$\displaystyle \theta$ + $\displaystyle \mbox{\boldmath$\bar{e}_z$}$cos$\displaystyle \beta$cos$\displaystyle \theta$)  
    + $\displaystyle \rho$sin t(- $\displaystyle \mbox{\boldmath$\bar{e}_x$}$cos$\displaystyle \beta$ - $\displaystyle \mbox{\boldmath$\bar{e}_y$}$cos$\displaystyle \alpha$sin$\displaystyle \beta$sin$\displaystyle \theta$ + $\displaystyle \mbox{\boldmath$\bar{e}_z$}$cos$\displaystyle \alpha$sin$\displaystyle \beta$cos$\displaystyle \theta$)  
    + $\displaystyle \rho$sin$\displaystyle \alpha$sin$\displaystyle \beta$($\displaystyle \mbox{\boldmath$\bar{e}_y$}$cos$\displaystyle \theta$ + $\displaystyle \mbox{\boldmath$\bar{e}_z$}$sin$\displaystyle \theta$) (6)

と表されることになる。今、
$\displaystyle \mbox{\boldmath$\mu$}$ = $\displaystyle \mbox{\boldmath$\bar{e}_y$}$cos$\displaystyle \theta$ + $\displaystyle \mbox{\boldmath$\bar{e}_z$}$sin$\displaystyle \theta$,   $\displaystyle \mbox{\boldmath$\xi$}$ = - $\displaystyle \mbox{\boldmath$\bar{e}_y$}$sin$\displaystyle \theta$ + $\displaystyle \mbox{\boldmath$\bar{e}_z$}$cos$\displaystyle \theta$ (7)
とすると、 $ \mu$ , $ \xi$ は、 $ \bar{{e}}_{y}^{}$ , $ \bar{{e}}_{z}^{}$ の含まれる平面上、 これらのベクトルを $ \bar{{e}}_{y}^{}$ から $ \bar{{e}}_{z}^{}$ の方向へ それぞれ $ \theta$ だけ回転したものに等しい (図 6)。
図 6: $ \mu$ と $ \xi$
\includegraphics[height=0.2\textheight]{muxi.eps}

よって、 $ \bar{{e}}_{x}^{}$ , $ \mu$ , $ \xi$ は 互いに垂直な単位ベクトルで、 $ \xi$ = $ \bar{{e}}_{x}^{}$ x $ \mu$ となる。 この $ \mu$ , $ \xi$ を用いれば、(6) は、

$\displaystyle \overrightarrow{\mbox{\rm OQ}}$ = $\displaystyle \rho$cos t($\displaystyle \mbox{\boldmath$\bar{e}_x$}$cos$\displaystyle \alpha$sin$\displaystyle \beta$ + $\displaystyle \mbox{\boldmath$\xi$}$cos$\displaystyle \beta$) + $\displaystyle \rho$sin t(- $\displaystyle \mbox{\boldmath$\bar{e}_x$}$cos$\displaystyle \beta$ + $\displaystyle \mbox{\boldmath$\xi$}$cos$\displaystyle \alpha$sin$\displaystyle \beta$)  
    + $\displaystyle \rho$$\displaystyle \mbox{\boldmath$\mu$}$sin$\displaystyle \alpha$sin$\displaystyle \beta$  
  = $\displaystyle \rho$$\displaystyle \mbox{\boldmath$\bar{e}_x$}$(cos$\displaystyle \alpha$sin$\displaystyle \beta$cos t - cos$\displaystyle \beta$sin t) + $\displaystyle \rho$$\displaystyle \mbox{\boldmath$\xi$}$(cos$\displaystyle \beta$cos t + cos$\displaystyle \alpha$sin$\displaystyle \beta$sin t)  
    + $\displaystyle \rho$$\displaystyle \mbox{\boldmath$\mu$}$sin$\displaystyle \alpha$sin$\displaystyle \beta$  

と書ける。この式の cos t , sin t の係数を見るとわかるが、

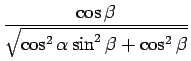
cos$\displaystyle \gamma$ = $\displaystyle {\frac{{\cos\alpha\sin\beta}}{{\sqrt{\cos^2\alpha\sin^2\beta+\cos^2\beta}}}}$,   sin$\displaystyle \gamma$ = $\displaystyle {\frac{{\cos\beta}}{{\sqrt{\cos^2\alpha\sin^2\beta+\cos^2\beta}}}}$

となる $ \gamma$ を取って合成すれば、

$\displaystyle \overrightarrow{\mbox{\rm OQ}}$ = $\displaystyle \rho$$\displaystyle \sqrt{{\cos^2\alpha\sin^2\beta+\cos^2\beta}}${$\displaystyle \mbox{\boldmath$\bar{e}_x$}$cos(t + $\displaystyle \gamma$) + $\displaystyle \mbox{\boldmath$\xi$}$sin(t + $\displaystyle \gamma$)} + $\displaystyle \rho$$\displaystyle \mbox{\boldmath$\mu$}$sin$\displaystyle \alpha$sin$\displaystyle \beta$

と書けることがわかる。よって、 $ \overrightarrow{\mbox{\rm PO}}$ は (5) より
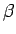
$\displaystyle \overrightarrow{\mbox{\rm PO}}$ = - $\displaystyle \rho$$\displaystyle \mbox{\boldmath$\mu$}$sin$\displaystyle \alpha$sin$\displaystyle \beta$ - r$\displaystyle \mbox{\boldmath$\bar{e}_z$}$  
    - $\displaystyle \rho$$\displaystyle \sqrt{{\cos^2\alpha\sin^2\beta+\cos^2\beta}}${$\displaystyle \mbox{\boldmath$\bar{e}_x$}$cos(t + $\displaystyle \gamma$) + $\displaystyle \mbox{\boldmath$\xi$}$sin(t + $\displaystyle \gamma$)} (8)

と書けることになる。 今、

$\displaystyle \overrightarrow{\mbox{\rm PS}}$ = - $\displaystyle \rho$$\displaystyle \mbox{\boldmath$\mu$}$sin$\displaystyle \alpha$sin$\displaystyle \beta$ - r$\displaystyle \mbox{\boldmath$\bar{e}_z$}$,   R = $\displaystyle \rho$$\displaystyle \sqrt{{\cos^2\alpha\sin^2\beta+\cos^2\beta}}$,   $\displaystyle \gamma{^\prime}$ = $\displaystyle \gamma$ + $\displaystyle \pi$

と書くことにすれば、(8) は、
$\displaystyle \overrightarrow{\mbox{\rm PO}}$ = $\displaystyle \overrightarrow{\mbox{\rm PS}}$ + R{$\displaystyle \mbox{\boldmath$\bar{e}_x$}$cos(t + $\displaystyle \gamma{^\prime}$) + $\displaystyle \mbox{\boldmath$\xi$}$sin(t + $\displaystyle \gamma{^\prime}$)} (9)
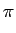
となる。つまり t を動かしたときの P から見た太陽の中心 O の軌道は、 点 S を中心とし、S を通り $ \bar{{e}}_{x}^{}$ , $ \xi$ に平行な平面上で 半径 R の円運動 ( $ \bar{{e}}_{x}^{}$ から $ \xi$ へ向かう方向への回転) をすることになる。

次へ: 6 公転による変化 上へ: 春分について 前へ: 4 観測点での座標系
竹野茂治＠新潟工科大学
2008年3月24日