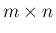
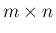 行列
行列
![$S=[s_{i,j}]_{m,n}$](img221.png) で説明する。
で説明する。
添字の部分列を
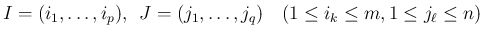
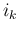 は互いに異なり、
は互いに異なり、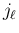 も互いに異なるとし、
通常は昇順に単調、すなわち
も互いに異なるとし、
通常は昇順に単調、すなわち
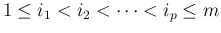 であることが
多いが、一般には単調性は仮定しない。
昇順に単調な場合を「昇順な添字列」と呼ぶことにする。
また、
であることが
多いが、一般には単調性は仮定しない。
昇順に単調な場合を「昇順な添字列」と呼ぶことにする。
また、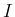 の
の 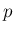 、
、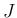 の
の 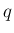 をこの添字列の「長さ」とする。
をこの添字列の「長さ」とする。
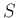 の
の
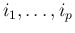 行目、
行目、
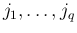 列目の要素を順に
並べた
列目の要素を順に
並べた 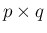 の小行列を
の小行列を
![$\displaystyle S^{I}_{J} = S^{(i_1,\ldots,i_p)}_{(j_1,\ldots,j_q)}
=\left[\begin...
...}\\
\vdots & & \vdots\\ s_{i_p,j_1} & \cdots & s_{i_p,j_q}\end{array}\right]
$](img234.png)
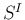 ,
, 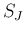 のように使うこともあるが、
のように使うこともあるが、
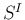 は
は 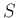 の
の
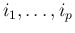 行目を上から順に並べた行列、
行目を上から順に並べた行列、
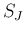 は
は 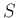 の
の
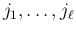 列目を左から順に並べた行列となる。
列目を左から順に並べた行列となる。
また、![$[I]$](img238.png) で、
で、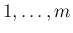 から
から
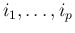 を取り除いた
昇順な添字列を表し、
を取り除いた
昇順な添字列を表し、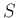 から
から
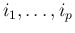 行目、
行目、
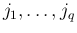 列目
を取り除いた
列目
を取り除いた
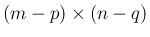 の小行列を
の小行列を
![$\displaystyle S^{[I]}_{[J]} = S^{[i_1,\ldots,i_p]}_{[j_1,\ldots,j_q]}
$](img241.png)
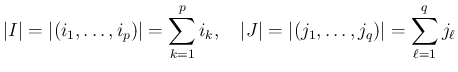
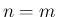 の場合の
の場合の  の
の  余因子は、
と書け、
余因子は、
と書け、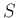 の余因子行列
の余因子行列 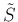 は
で、
は
で、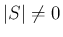 の場合の
の場合の 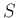 の逆行列は
となる。
の逆行列は
となる。
(40) より、余因子行列 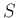 の成分、
すなわち 1 次の小行列式は、
の成分、
すなわち 1 次の小行列式は、
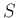 の
の 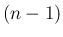 次の小行列式に符号をつけたもの
次の小行列式に符号をつけたもの
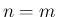 で、
で、
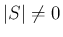 のとき、長さ
のとき、長さ 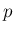 (
(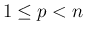 ) の
昇順な添字列
) の
昇順な添字列 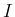 ,
, 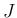 に対して次が成り立つ。
に対して次が成り立つ。
(42) は、(43) の 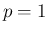 の場合になっていて、
よって命題 2 は (42) の
拡張になっている。
この命題 2 の証明の前に、次の補題を紹介する。
の場合になっていて、
よって命題 2 は (42) の
拡張になっている。
この命題 2 の証明の前に、次の補題を紹介する。
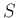 を
を 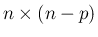 行列、
行列、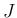 を 1 から
を 1 から 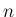 の範囲の長さ
の範囲の長さ 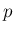 の
昇順の添字列、
の
昇順の添字列、
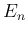 を
を 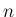 次正方行列とするとき、
次正方行列とするとき、
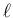 ,
, 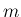 は
は
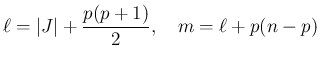
証明
![$\displaystyle E_n = \left[\begin{array}{ccc}\overrightarrow{e}_1&\cdots&\overri...
...\overrightarrow{s}_{n-p}\end{array}\right],
\hspace{0.5zw}J=(j_1,\ldots,j_p)
$](img258.png)
![\begin{eqnarray*}\vert(E_n)_J\hspace{0.5zw}S\vert
&=&
\left\vert\begin{array}...
...\ &=&
\cdots
\ =\
(-1)^{\ell'}\left\vert S^{[J]}\right\vert
\end{eqnarray*}](img259.png)
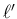 は、
は、
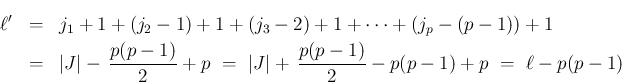
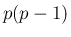 は偶数なので
は偶数なので
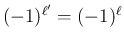 となって、
(44) の前半が示されたことになる。
後半は、行列式の列の入れ替えを行えば、
となって、
(44) の前半が示されたことになる。
後半は、行列式の列の入れ替えを行えば、
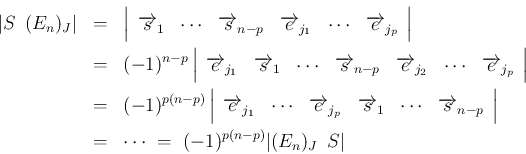
命題 2 の証明
![$\displaystyle \tilde{S}
=\left[\begin{array}{ccc}\overrightarrow{\tilde{s}}_1&\cdots\overrightarrow{\tilde{s}}_n\end{array}\right]
$](img265.png)
![$[I]=(i_1',\ldots,i_{n-p}')$](img266.png) とし、
とし、
![$\displaystyle C
=[\tilde{S}_J\hspace{0.5zw}(E_n)_{[I]}]
=\left[\begin{array}{...
...errightarrow{e}_{i_1'}&\cdots&\overrightarrow{e}_{i_{n-p}'}\end{array}\right]
$](img267.png)
 より、
より、
![\begin{eqnarray*}SC
&=&
\left[\begin{array}{cccccc}\vert S\vert\overrightarrow...
...rt S\vert\left[(E_n)_J\hspace{0.5zw}S_{[I]}/\vert S\vert\right]
\end{eqnarray*}](img270.png)
![\begin{eqnarray*}\vert SC\vert
&=&
\vert S\vert^n\left\vert(E_n)_J\hspace{0.5z...
...=\
(-1)^\ell\vert S\vert^p\left\vert S_{[I]}^{[J]}\right\vert
\end{eqnarray*}](img271.png)
 である。
また、
である。
また、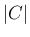 については、再び補題 3 より
については、再び補題 3 より
![$\displaystyle \vert C\vert
=\left\vert\tilde{S}_J\hspace{0.5zw}(E_n)_{[I]}\right\vert
=(-1)^m\left\vert\tilde{S}^{I}_J\right\vert
$](img274.png)
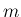 は
は
![$\displaystyle m = \vert[I]\vert + \frac{(n-p)(n-p+1)}{2}+(n-p)p
= \vert[I]\vert + \frac{(n-p)(n+p+1)}{2}
$](img275.png)
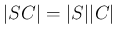 より、
より、
![$\displaystyle \left\vert\tilde{S}^{I}_J\right\vert
=(-1)^{\ell-m}\vert S\vert^{p-1}\left\vert S_{[I]}^{[J]}\right\vert
$](img277.png)
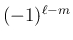 を考えればよい。
を考えればよい。
![\begin{eqnarray*}\ell-m
&=&
\vert J\vert+\frac{p(p+1)}{2}-\vert[I]\vert - \,\f...
...,-\,\frac{(n-p)(n+p+1)}{2}
\\ &=&
\vert I\vert+\vert J\vert+k
\end{eqnarray*}](img279.png)
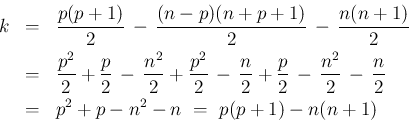
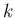 は偶数なので
は偶数なので
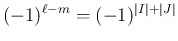 となって、これで (43) が示されたことになる。
となって、これで (43) が示されたことになる。
命題 2 と同じ仮定の元、
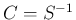 とすると、
とすると、
![$\displaystyle \left\vert C^{I}_{J}\right\vert
=\frac{(-1)^{\vert I\vert+\vert J\vert}}{\vert S\vert}\left\vert S^{[J]}_{[I]}\right\vert
$](img283.png)
![$\displaystyle \left\vert S^{I}_{J}\right\vert
=\frac{(-1)^{\vert I\vert+\vert ...
...1)^{\vert I\vert+\vert J\vert}\vert S\vert\left\vert C^{[J]}_{[I]}\right\vert
$](img284.png)
証明
![$\displaystyle \vert[I]\vert=\frac{n(n+1)}{2}-\vert I\vert,
\hspace{1zw}
\vert[J]\vert=\frac{n(n+1)}{2}-\vert J\vert
$](img285.png)
![$(-1)^{\vert[I]\vert+\vert[J]\vert}=(-1)^{\vert I\vert+\vert J\vert}$](img286.png) 、
、
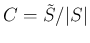 より、
いずれも命題 2 から容易に得られる。
より、
いずれも命題 2 から容易に得られる。
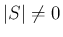 の仮定を外しても命題 2 は成立する。
の仮定を外しても命題 2 は成立する。
証明
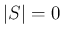 のときにも (43) が
成り立つことを示せばよい。
のときにも (43) が
成り立つことを示せばよい。
今、
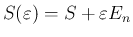 とすると、
とすると、
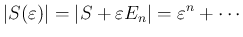
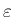 の
の 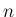 次式であり、
次式であり、
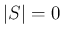 と仮定すると
と仮定すると 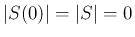 となるが、
となるが、
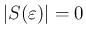 となる
となる 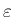 は高々
は高々 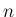 個なので、
集積点はなく、よって
個なので、
集積点はなく、よって
「となるようなでは
と なる
は
のみ」
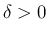 を取ることができる。
よって、
を取ることができる。
よって、
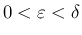 では
では
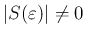 だから
だから
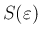 に対して命題 2 が成立し、
が成り立つ。ここにでてくる行列式はいずれも
に対して命題 2 が成立し、
が成り立つ。ここにでてくる行列式はいずれも 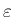 の多項式、
よって
の多項式、
よって 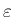 の連続関数で、
の連続関数で、
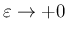 のときに
明らかに
のときに
明らかに
![$\displaystyle \left\vert\widetilde{S(\varepsilon)}^{I}_{J}\right\vert\rightarro...
...silon)^{[J]}_{[I]}\right\vert
\rightarrow\left\vert S^{[J]}_{[I]}\right\vert
$](img302.png)
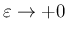 とすれば、
とすれば、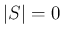 のときの (43) が得られる。
のときの (43) が得られる。
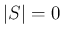 の場合は、実際には (43) は、
の場合は、実際には (43) は、
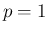 ならば (42) であるから証明は不要で、
よって
ならば (42) であるから証明は不要で、
よって 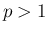 の場合に
の場合に
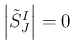 と
なることだけ示せばいいので、このような解析的な証明ではなく、
代数的なより易しい証明があるかもしれない。
と
なることだけ示せばいいので、このような解析的な証明ではなく、
代数的なより易しい証明があるかもしれない。
なお、この後の議論では、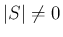 が保証されていない状態で (43) を使う場面がでてくるので、
この系 5 の形に命題 2 を
拡張しておく必要があるのである。
が保証されていない状態で (43) を使う場面がでてくるので、
この系 5 の形に命題 2 を
拡張しておく必要があるのである。
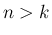 、および
、および 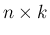 行列
行列
![$S=\left[\begin{array}{ccc}\overrightarrow{s}_1&\cdots&\overrightarrow{s}_k\end{array}\right]$](img307.png) に対し、
に対し、
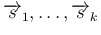 が線形独立であることと、
が線形独立であることと、
![$\displaystyle
\vert{}^t{S}S\vert=\left\vert\left[\overrightarrow{s}_i\mathrel{・}\overrightarrow{s}_j\right]_{k,k}\right\vert>0
$](img309.png) であることは同値。
であることは同値。
証明
行列式の展開定理により、
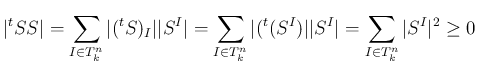
 は 1 から
は 1 から  までの範囲の、
長さ
までの範囲の、
長さ 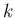 の昇順の添字列全体の集合。
の昇順の添字列全体の集合。
よって、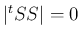 であることはすべての
であることはすべての 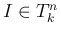 に
対して
に
対して 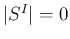 であることと同値で、
これは
であることと同値で、
これは
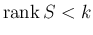 を意味し、そしてこれは
を意味し、そしてこれは 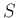 の列ベクトルが
線形従属であることと同値。
の列ベクトルが
線形従属であることと同値。
竹野茂治@新潟工科大学