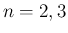
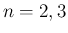 の場合と同様に、
の場合と同様に、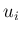 を
を 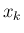 の一次式として、
とする。この
の一次式として、
とする。この 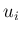 が
が
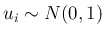 となるためには、
[2] より
となるためには、
[2] より
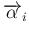 ,
,
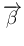 を
とすると、条件 (8), (9) は
と書け、つまり
を
とすると、条件 (8), (9) は
と書け、つまり
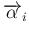 はすべて
はすべて
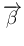 と垂直な
単位ベクトルとなる。
なお、
と垂直な
単位ベクトルとなる。
なお、
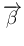 も単位ベクトルである。
も単位ベクトルである。
また、
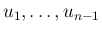 が独立であることは、
[3] により、
が独立であることは、
[3] により、
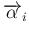 (
(
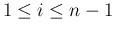 ) が
互いに垂直であることと同値である。
よって、これらをまとめると、
) が
互いに垂直であることと同値である。
よって、これらをまとめると、
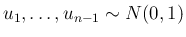 で、
かつ独立であることは、
で、
かつ独立であることは、
「と同値になる。そしてこれは、行列が 互いに垂直な単位ベクトル」
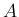 を
とすれば、
を
とすれば、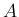 が直交行列、すなわち
となることと同値になる (
が直交行列、すなわち
となることと同値になる (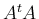 は
は 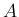 の行ベクトルの内積を
成分とする行列)。
の行ベクトルの内積を
成分とする行列)。
竹野茂治@新潟工科大学