2 方向微分係数
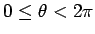 に対して (実際は後で述べるように
に対して (実際は後で述べるように
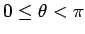 でよい)、
でよい)、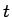 の関数
の関数 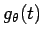 を、
を、
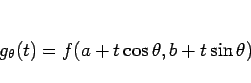 |
(3) |
と定める。点
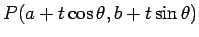 は、
点
は、
点 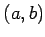 から
から 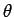 方向 (動径ベクトル
方向 (動径ベクトル
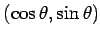 の方向) に伸びる直線
の方向) に伸びる直線 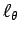 上を、
上を、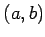 から距離
から距離 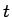 だけ進んだ点 (図 1) であり、
よって (3) は、
だけ進んだ点 (図 1) であり、
よって (3) は、
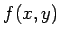 の
の 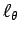 上の値だけを見た 1 変数関数、ということになる。
上の値だけを見た 1 変数関数、ということになる。
図 1:
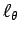 と
と 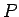
|
|
この 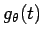 の微分係数を、
の微分係数を、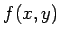 の
の 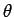 方向への
方向微分係数 と呼ぶ。
方向への
方向微分係数 と呼ぶ。
合成関数の微分 ([1] 定理 34.1) により、
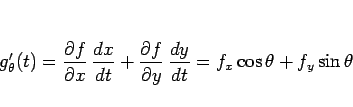 |
(4) |
となるから、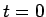 とすると
とすると 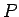 は
は 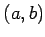 となり、
仮定 (1) より、
となり、
仮定 (1) より、
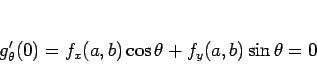
となる。
(4) をさらに微分すると、
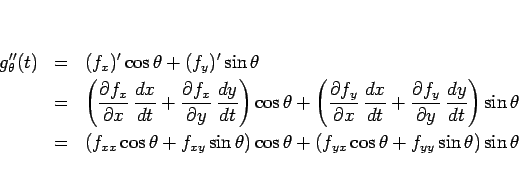
となるので、偏微分の順序交換の定理 ([1] 定理 33.1)、
および仮定 (2) より、
となることがわかる。
竹野茂治@新潟工科大学
2014年11月14日
![]() の微分係数を、
の微分係数を、![]() の
の ![]() 方向への
方向微分係数 と呼ぶ。
方向への
方向微分係数 と呼ぶ。