4 三角関数の有理関数の積分
次は、三角関数の含まれる有理関数の積分、例えば
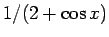 のようなものの不定積分を考える。
少し一般化して、
のようなものの不定積分を考える。
少し一般化して、
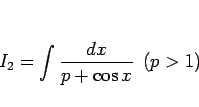 |
(13) |
を考えることにする。
この積分の標準的な求め方は、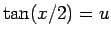 (
(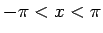 ) とする
割と面倒な置換積分であるが、
) とする
割と面倒な置換積分であるが、
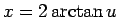 より
より
となるので、
となる。ここで
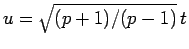 とすれば
とすれば
となり、結局
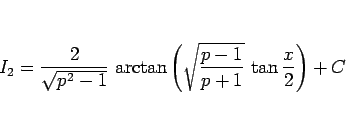 |
(14) |
が得られる。
ただし、(14) は、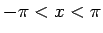 で考えていて、
より広い範囲で考えると (14) の右辺は
で考えていて、
より広い範囲で考えると (14) の右辺は 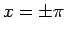 では
不連続になってしまう。
一方で、定義 (13) よりわかるが、
では
不連続になってしまう。
一方で、定義 (13) よりわかるが、
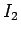 はすべての
はすべての 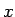 で連続につながる原始関数を持つはずなので、
ここでそれを先に考えておく。
で連続につながる原始関数を持つはずなので、
ここでそれを先に考えておく。
そのために、定数 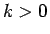 に対し、
以下のような関数
に対し、
以下のような関数 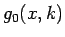 ,
, 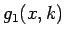 を考える。
を考える。
なお、
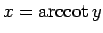 は
は 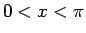 での
での 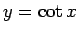 (図 1) の逆関数で、すべての実数
(図 1) の逆関数で、すべての実数  で定義され、
で定義され、
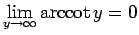 ,
,
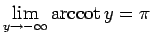 となるもの (図 2)、
また
となるもの (図 2)、
また 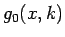 ,
, 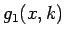 の定義域は、
それぞれ
の定義域は、
それぞれ 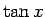 ,
, 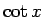 の定義域と同じものとする。
の定義域と同じものとする。
図 1:
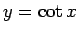 のグラフ
のグラフ
|
|
図 2:
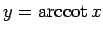 のグラフ
のグラフ
|
|
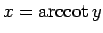 とすると、
とすると、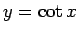 (
(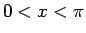 ) で、
) で、
で、
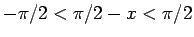 より
より
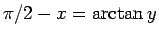 となるから、よって
となるから、よって
となる。これにより、
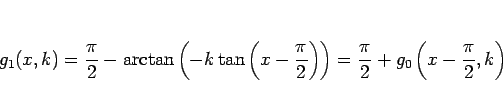 |
(17) |
となるので、
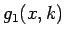 のグラフは、
のグラフは、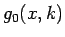 のグラフを平行移動したもの
になる (図 3)。
のグラフを平行移動したもの
になる (図 3)。
いずれも周期は 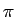 、そして
、そして 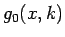 は奇関数で、
は奇関数で、
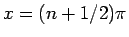 (
(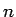 は整数) で不連続:
は整数) で不連続:
となっている。
また、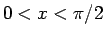 では、
では、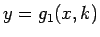 とすると
とすると 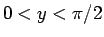 で、
で、
となり、よって 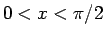 では
では
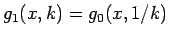 が
成り立つことがわかる。
が
成り立つことがわかる。
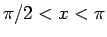 では、この性質と周期性、および (17) により
では、この性質と周期性、および (17) により
となる。
ここから、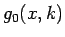 ,
, 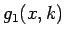 の段差を解消した関数 (図 4):
の段差を解消した関数 (図 4):
は、いずれも連続で (定義域の境界では極限で考える)、
上の考察からすべての 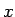 に対して
に対して
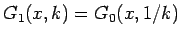 で
あることがわかり、よって、すべての
で
あることがわかり、よって、すべての 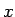 で滑らかであることもわかる。
で滑らかであることもわかる。
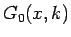 の導関数は、
の導関数は、
なので、
となり、よって (13) の滑らかな原始関数による積分は、
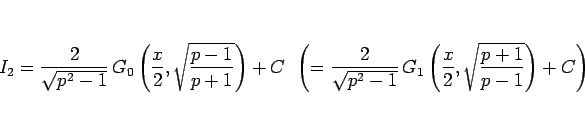 |
(18) |
であることがわかる。これが、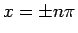 で不連続性の
段差を持つ (14) を、
すべての
で不連続性の
段差を持つ (14) を、
すべての 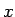 に対して滑らかに拡張したものになる。
に対して滑らかに拡張したものになる。
竹野茂治@新潟工科大学
2016年12月22日
![]() (
(![]() ) とする
割と面倒な置換積分であるが、
) とする
割と面倒な置換積分であるが、
![]() より
より
![]() で考えていて、
より広い範囲で考えると (14) の右辺は
で考えていて、
より広い範囲で考えると (14) の右辺は ![]() では
不連続になってしまう。
一方で、定義 (13) よりわかるが、
では
不連続になってしまう。
一方で、定義 (13) よりわかるが、
![]() はすべての
はすべての ![]() で連続につながる原始関数を持つはずなので、
ここでそれを先に考えておく。
で連続につながる原始関数を持つはずなので、
ここでそれを先に考えておく。
![]() に対し、
以下のような関数
に対し、
以下のような関数 ![]() ,
, ![]() を考える。
を考える。
![]() 、そして
、そして ![]() は奇関数で、
は奇関数で、
![]() (
(![]() は整数) で不連続:
は整数) で不連続:
![]() では、
では、![]() とすると
とすると ![]() で、
で、
![]() ,
, ![]() の段差を解消した関数 (図 4):
の段差を解消した関数 (図 4):
![]() の導関数は、
の導関数は、