整式 ![]() を整式
を整式 ![]() で割った余りを
で割った余りを ![]() とするとき、
とするとき、
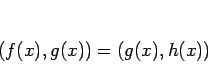
なお、![]() は、
は、![]() と
と ![]() の
最大次数の共通因子 (最大公約数) を表すこととするが、
例えば
の
最大次数の共通因子 (最大公約数) を表すこととするが、
例えば ![]() の場合、
の場合、![]() は 1 次式の共通因子であるし、
は 1 次式の共通因子であるし、
![]() も同じ次数の共通因子なので、
これを一つに確定するために、
も同じ次数の共通因子なので、
これを一つに確定するために、![]() の最高次の係数は 1 であるとする
(よって例えば
の最高次の係数は 1 であるとする
(よって例えば ![]() とする)。
とする)。
補題 3 の証明
![]() を
を ![]() で割った商を
で割った商を ![]() とすると、
とすると、
今、
![]() とし、
とし、![]() ,
, ![]() を
を ![]() で割った商を
で割った商を
![]() ,
, ![]() とすると
とすると
![]() ,
,
![]() となるので、
(1) より
となるので、
(1) より
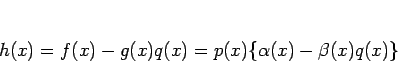
逆に、
![]() とし、
とし、![]() ,
, ![]() を
を ![]() で割った商を
で割った商を
![]() ,
, ![]() とすると、
とすると、
![]() ,
,
![]() となるので、
(1) より
となるので、
(1) より
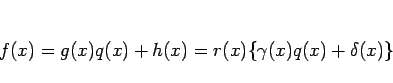
2 つの整式の共通因子を求める場合、補題 3 により、
![]() と
と ![]() の共通因子
の共通因子 ![]() を求めるときに、
を求めるときに、
![]() と
と ![]() の割り算を行って、
の割り算を行って、
![]() を求める代わりに
を求める代わりに ![]() を求めればよいことになる。
そして今度は
を求めればよいことになる。
そして今度は ![]() を
を ![]() で割った余り
で割った余り ![]() があれば、
があれば、
![]() を求める代わりに
を求める代わりに ![]() を求めればよい。
を求めればよい。
![]() は
は ![]() で割った余りなので少なくとも
で割った余りなので少なくとも ![]() であり、
この作業を繰り返すことで、計算する整式の次数は確実に下がっていく。
よって、最後は余りが 0 次式、すなわち定数になるが、
その定数が 0 に等しければ、最後の割り算は割り切れたことになるので、
その割った式が
であり、
この作業を繰り返すことで、計算する整式の次数は確実に下がっていく。
よって、最後は余りが 0 次式、すなわち定数になるが、
その定数が 0 に等しければ、最後の割り算は割り切れたことになるので、
その割った式が ![]()
![]() の共通因子となる。
その定数が 0 でなければ、0 以外の定数と整式の共通因子は 1 なので、
共通因子は 1 となり、すなわち
の共通因子となる。
その定数が 0 でなければ、0 以外の定数と整式の共通因子は 1 なので、
共通因子は 1 となり、すなわち ![]() と
と ![]() は互いに素であることになる。
は互いに素であることになる。
このようにして 2 つの整式の共通因子を求める方法が互除法である。