そこで、部分分数分解の原理として、私は例年次の定理、 そしてそこから得らえる系を紹介している。
整式 ![]() ,
, ![]() が
が ![]() (
(![]() は、整式
は、整式 ![]() の次数を意味する)
のとき、
の次数を意味する)
のとき、
![]() で整式
で整式 ![]() ,
, ![]() が互いに素ならば、
が互いに素ならば、
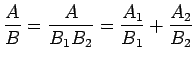
整式 ![]() ,
, ![]() が
が ![]() のとき、
のとき、
![]() で、
整式
で、
整式 ![]() ,
, ![]() , ...,
, ...,![]() がどの 2 つも互いに素ならば、
がどの 2 つも互いに素ならば、
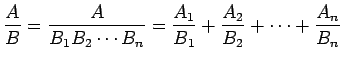
なお、2 つの整式 ![]() ,
, ![]() が 互いに素 であるとは、
1 次以上の共通因子 (
が 互いに素 であるとは、
1 次以上の共通因子 (![]() ,
, ![]() の両方を割り切る整式) が
存在しないことを意味する。
の両方を割り切る整式) が
存在しないことを意味する。
講義では、証明なしでこの定理を紹介しているだけだったので、 ここにその証明を簡単にまとめておくこととする。
なお、以下は実数係数の整式 (多項式) を考えることとするが、 有理数係数の整式に限定しても、あるいは複素数係数の整式に広げても 同じ論法が使える。