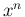
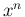 と
と 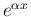 の積の積分
を考える。まず、簡単な置換により、
この積分は
の積の積分
を考える。まず、簡単な置換により、
この積分は 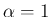 の場合に帰着できる。
の場合に帰着できる。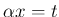 により、
となるからである。よってとりあえず、
により、
となるからである。よってとりあえず、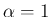 の場合を考える。
の場合を考える。
部分積分
により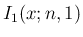 は、
は、
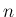 を一つ下げた積分に帰着でき、
これを繰り返すことで最終的に
を一つ下げた積分に帰着でき、
これを繰り返すことで最終的に
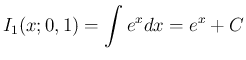
一方、(4) の式の両辺を 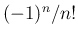 倍すれば、
倍すれば、
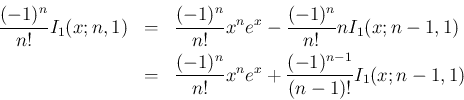
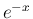 の
の 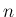 次のマクローリン展開式と、
次のマクローリン展開式と、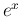 との
積の形になっているが、それについては、5 節で
改めて紹介する。
との
積の形になっているが、それについては、5 節で
改めて紹介する。
また、(2) を考えれば、
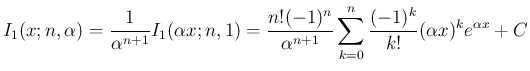
なお、(6) は、積の微分から得ることもできる。
今、
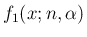 を
を

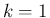 から
から 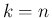 までの和に
までの和に
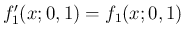 を
追加すれば、
を
追加すれば、
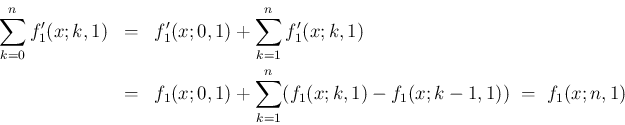
同様のことを
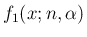 に行えば、以下のようになる。
に行えば、以下のようになる。
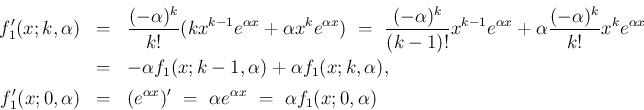
竹野茂治@新潟工科大学