次へ: 3 その他の誤答 上へ: 2 全般的な注意 前へ: 2.1 微分と代入の順序 (PDF ファイル: fortest2-2006.pdf)

2.2 従属変数

また、2. の $z(x,y)$ や $z(1,2)$ であるが、 これは場合によっては間違いとは言えないが、通常このような書き方はしない。

例えば一変数の関数の場合、$y=f(x)$ と書くが、 この場合、$y$ は従属変数、 つまり (独立変数) $x$ の値の変化によって値が変わるものを意味し、 関数 $f(x)$ の値域の集合のある値を取る変数であって関数ではない。

それに対して右辺の $f(x)$ の方は、$f$ が関数名であり、 その関数に $x$ という値を代入した状態を意味している。 名前の後に $(x)$ と書くのは、その名前のものが関数であることを表している。 $f(x)$ は $x$ の式であるが、本来 $y$ 自体が $x$ の式なのではなく、 $y$ はその $x$ の式によって値が定まるものである。

つまり $y$ 自体は、その $f(x)$ の値が代入されるが、 関数ではなく変数であるから普通 $y(x)$ とは書かない。

それと同様で、$z=f(x,y)$ と書けば、それは $z$ は、関数 $f$ の $x,y$ の値によって決定する値が代入される変数 (従属変数) を意味し、 $z$ 自体は関数ではない。

だから本来は $z(1,2)$ ではなく、$f(1,2)$ と書くべきで、 もし元の問題が $z=(x,y の式)$ のように与えられたのであれば、 講義中に説明した通り、一度「この右辺を $f(x,y)$ とすると」と書いて、 $f(x,y)$ という関数記号を導入した上で $f(1,2)$ と書くべきである。

ただし、一変数関数の場合の $y$ 自体、あるいは二変数関数の $z$ 自体を 関数と見ることは絶対にないかというと、 それには伝統に根ざした例外があり、実は $y'$ や $z_x$ という記号は、本来 $y$ 自体が $x$ の関数である、あるいは $z$ 自体が $x,y$ の関数であると見なした書き方である。

だから、必ずそういう見方はしない、というわけでもないが、 今回このような書き方が見られたのは接平面の問題であって、 接平面の場合は、$x,y,z$ という 3 次元の座標系でのグラフを扱うので、 $z$ を関数と見ると、それが軸の名前なのか、関数の名前なのかがややこしく、 そのように接平面の式を書いてしまうと

$$z-z(1,2)=z_x(1,2)(x-1)+z_y(1,2)(y-2)$$

となって、式の最初に現れる $z$ とその次の $z(1,2)$ の $z$ が 同じものを意味すると見えてしまう (最初の $z$ は座標、あるいは $x,y$ の従属変数としての $z$ であるが、 その次の $z(1,2)$ の $z$ はそれとは無関係の関数名としての $z$)。

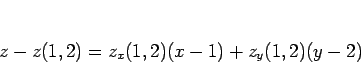
1 つの問題の中で、1 つの記号が 2 つの意味を持つような記法は 避けるべきであるから、この問題ではやはり、 「この右辺を $f(x,y)$ とすると」と書くべきだと思う。

次へ: 3 その他の誤答 上へ: 2 全般的な注意 前へ: 2.1 微分と代入の順序