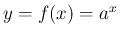 とすると、この関数のグラフを
とすると、この関数のグラフを 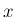 方向に
方向に 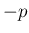 移動すると、
それは元のグラフを
移動すると、
それは元のグラフを 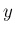 方向に
方向に 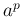 倍したことに等しくなる (図 3)。すなわち、
倍したことに等しくなる (図 3)。すなわち、
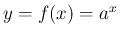 とすると、この関数のグラフを
とすると、この関数のグラフを 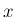 方向に
方向に 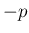 移動すると、
それは元のグラフを
移動すると、
それは元のグラフを 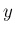 方向に
方向に 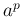 倍したことに等しくなる (図 3)。すなわち、
倍したことに等しくなる (図 3)。すなわち、
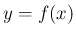 の
の 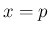 での傾き
での傾き 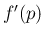 は、
そのままグラフを
は、
そのままグラフを 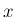 方向に
方向に 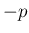 平行移動しても傾きは変わらず、
それが
平行移動しても傾きは変わらず、
それが 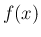 の
の 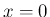 での
での 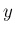 方向の
方向の 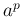 倍のグラフに一致するので、
倍のグラフに一致するので、
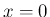 での傾きの
での傾きの 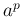 倍に等しいことになる。
すなわち、
倍に等しいことになる。
すなわち、
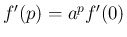 が成り立ち、
よって一般に
となる。
が成り立ち、
よって一般に
となる。
なお、この式はグラフによらなくても (7) を 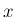 で
微分して
で
微分して 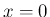 とすることでも得られる。
とすることでも得られる。
あとは、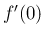 だけ求めればよいのであるが、この値は
だけ求めればよいのであるが、この値は 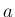 によって
変動し、丁度
によって
変動し、丁度 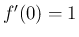 となるのが
となるのが 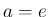 の場合であり、
それと (8) により公式 1 が成り立つことになる。
の場合であり、
それと (8) により公式 1 が成り立つことになる。
実際、(5) の左辺は 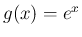 の
の 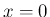 での
微分係数
での
微分係数 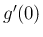 の定義と同じ式であり、
つまり (5) は
の定義と同じ式であり、
つまり (5) は 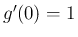 を示しているが、
それが導かれる経路を考えると、実は元々
を示しているが、
それが導かれる経路を考えると、実は元々 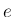 という定数の定義は、
この
という定数の定義は、
この 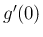 が 1 となるような底であると見ることもできる。
つまり、「
が 1 となるような底であると見ることもできる。
つまり、「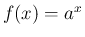 に対し
に対し 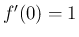 となる
となる 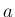 」が
」が 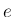 の定義で、
その定義と公式 1 は (8) によりほぼ直結することになる。
の定義で、
その定義と公式 1 は (8) によりほぼ直結することになる。
さて、一般の 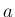 に対する公式 3 も、グラフの拡大の考え方で、
この公式 1 から導いてみよう。
上と同じく
に対する公式 3 も、グラフの拡大の考え方で、
この公式 1 から導いてみよう。
上と同じく 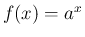 ,
, 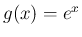 とする。
とする。
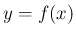 のグラフを
のグラフを 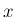 方向に
方向に 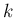 (
(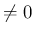 ) 倍すると、その関数は
) 倍すると、その関数は
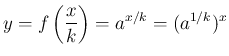
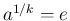 となる
となる 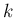 があれば、
これは
があれば、
これは 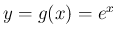 に一致することになる。
この
に一致することになる。
この 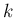 は、
は、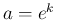 より
より
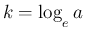 と求まり、
そしてこの
と求まり、
そしてこの 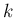 に対して
に対して 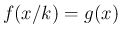 となる (図 4)。
となる (図 4)。
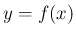 の
の
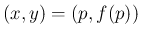 での傾き
での傾き 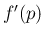 は、
そのグラフを
は、
そのグラフを 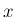 方向に
方向に 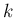 倍した
倍した 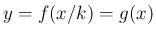 のグラフでは、
のグラフでは、
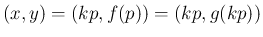 での傾きに対応するが、
その傾きは
での傾きに対応するが、
その傾きは 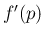 の
の 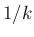 倍となる。
すなわち、
倍となる。
すなわち、
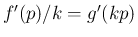 となるので、公式 1 により
となるので、公式 1 により
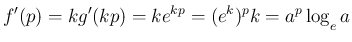
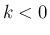 の場合も成立することに注意せよ。
の場合も成立することに注意せよ。
ちなみに、(4) の左辺も、
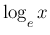 の
の 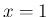 での微分係数を意味していて、
そして対数関数の導関数が
での微分係数を意味していて、
そして対数関数の導関数が 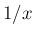 の定数倍であることも、
指数関数の場合と同様に得られる。
の定数倍であることも、
指数関数の場合と同様に得られる。
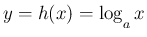 とすると、
このグラフを
とすると、
このグラフを 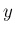 方向に
方向に 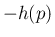 下げると、
それは元のグラフの
下げると、
それは元のグラフの 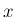 方向の
方向の 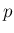 倍に対応する。
倍に対応する。
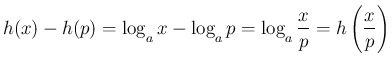
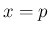 での
での 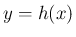 の傾き
の傾き 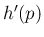 は、
は、
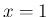 での傾き
での傾き 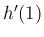 の
の 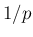 倍となる。
すなわち
倍となる。
すなわち 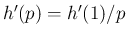 より
より
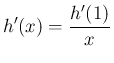
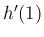 が 1 となるのが
が 1 となるのが 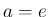 のときであり、
一般には
のときであり、
一般には
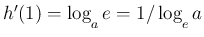 となるが、
それも指数関数の場合と同様に示される。
となるが、
それも指数関数の場合と同様に示される。
竹野茂治@新潟工科大学